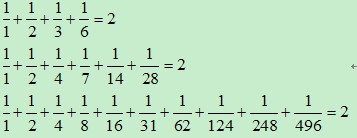一个自然数的所有因数的和,刚好等于这个数的2 倍,或者说一个自然数的所有的真因子(即除了本身以外的因数)的和,恰好等于它本身,这样的自然数,数学家给它起了一个美丽而动听的名字:完美的数!后来又称为完全数。例如6,它有因数1、2、3、6,除去它本身6 外,其余3 个数相加,l+2+3=6,所以6 是完全数。
又如28,除去本身28 外,它有5 个因数:1、2、4、7、14,而1+2+4+7+14=28。所以28 是完全数。
再如496,它的因数(本身除外)相加,1+2+4+8+16+31+62+124+248=496,所以496 也是一个完全数。再一个是:8128=1+2+4+8+16+32+64+127+254+508+1016+2032+4064。
这4 个完全数的发现,还是很早以前的事。起先人们认为这4 个数之间的间隔不算太大,可能存在不少的完全数。当人们找到第5个完全数时,竟相隔了一千多年, 直到1461 年才发现了33550336。一直到16 世纪末又发现了另外3个完全数。而第9个完全数到19 世纪才被发现,它竟是一个37位数。有些数学家曾探索寻找完全数的规律,虽然曾取得一点进展,但实际作用不大。完全数究竟是有限个数,还是无穷多?至今没有定论!
完全数有许多奇妙的性质。比如每一个完全数都可以写成连续自然数之和:
6=1+2+3;
28=1+2+3+4+5+6+7;
496=1+2+3+…+30+31。
除6 以外的完全数,还可以表示成奇数连乘积的和;如:
28=1×1×1+3×3×3;
496=1×1×1+3×3×3+5×5×5+7×7×7。
人们还发现,每一个完全数的所有因数(包括本身)的倒数之和,都等于2。如: