第三单元全练全测 - 精版答案
第1题
1.圆锥 高 底面半径
2.423.9
3.28.26 282.6
4.3943.84 4571.84
5.2 cm2
第2题
1.√
2.√
3.×
4.×
5.×
第3题
1.A
2.B D
3.D
※【浙江专用】A
4.C
第4题
1.3.14×(6÷2)2×8×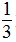 =75.36(dm3)
=75.36(dm3)
2.
表面积:10×10×5+3.14×(10÷2)2+3.14×10×10÷2=735.5(cm2)
体积:10×10×10+3.14×(10÷2)2×10÷2=1392.5(cm3)
第5题
1.半小时是30分钟。3.14×1.2×20×30=2260.8(m2)
2.200÷[3.14×(5÷2)2]≈10(dm)
3.
面积:3.14×6×5=94.2(cm2)
体积:3.14×(6÷2)2×15=423.9(cm3)
4.
方法一
分析:已知圆锥形黄豆堆的底面周长和高,可以求出这个圆锥形黄豆堆的底面半径和它的体积。把圆柱形粮仓的体积看作单位“1”,那么圆锥形黄豆堆的体积正好是圆柱形粮仓体积的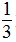 ,求单位“1”用除法计算。根据圆柱的体积公式,已知体积与高,可以求出底面积。
,求单位“1”用除法计算。根据圆柱的体积公式,已知体积与高,可以求出底面积。
解答:
分步列式:
15.7÷3.14÷2=2.5(m)……(3分)
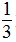 ×3.14×2.52×1.8÷
×3.14×2.52×1.8÷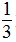 ÷2.5=14.13(m2)……(5分)
÷2.5=14.13(m2)……(5分)
综合列式:
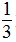 ×3.14×
×3.14×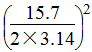 ×1.8÷
×1.8÷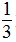 ÷2.5……(5分)
÷2.5……(5分)
=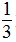 ×3.14×6.25×1.8÷
×3.14×6.25×1.8÷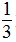 ÷2.5………………(2分)
÷2.5………………(2分)
=14.13(m2)……(1分)
答:其底面积是14.13平方米。……(1分)
方法二
分析:根据圆锥形黄豆堆的体积正好是圆柱形粮仓体积的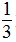 可以列出方程。假设圆柱形粮仓的底面积为x m2,则列方程为
可以列出方程。假设圆柱形粮仓的底面积为x m2,则列方程为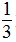 ×3.14×
×3.14×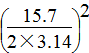 ×1.8=
×1.8=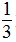 ×2.5x,解得x=14.13,所以圆柱形粮仓的底面积是14.13 m2。
×2.5x,解得x=14.13,所以圆柱形粮仓的底面积是14.13 m2。
解答:解:设其底面积为x m2。……(2分)
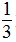 ×3.14×
×3.14×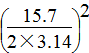 ×1.8=
×1.8=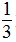 ×2.5x……(4分)
×2.5x……(4分)
x=14.13……(2分)
答:其底面积是14.13平方米。……(1分)
5.方法一
分析:因为胶水瓶正放和倒放时胶水瓶的容积与胶水的体积不变,所以两个瓶子空余部分的容积相等。因此胶水瓶的容积就相当于图(1)中胶水的体积加上图(2)中空余部分的体积,即一个高为8+2=10(cm)的圆柱形容器的容积,由此可知胶水的体积占瓶子容积的 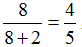 ,即35mL的
,即35mL的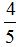 。
。
解答:
35mL=35cm3
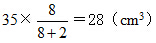 ……(8分)
……(8分)
答:瓶内胶水的体积是28立方厘米。……(1分)
方法二
分析:因为瓶子空余部分的容积相等,所以胶水的体积与瓶子空余部分的体积比是8∶2=4∶1,胶水的体积占胶水瓶容积的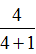 =
=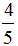 ,即35mL的
,即35mL的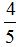 。
。
解答:35 mL=35cm3 35×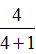 =28(cm3)………………(8分)
=28(cm3)………………(8分)
答:瓶内胶水的体积是28立方厘米。……(1分)
