(二)图形与几何 - 1.图形的认识与测量
(1)图形的认识与测量
第1题
(1)C A B
(2)C A
(3)C
(4)C
第3题
②⑦
④⑤
①⑧
③⑥
第4题
(1)65
(2)60
(3)直角
(4)锐角
(5)稳定
第5题
(1)易变形
(2)平行四边形 小
(3)平行四边形
第6题
(1)× (2)√ (3)×
第7题
分析:此题考查的是三角形、平行四边形、长方形、梯形面积的计算。要明确不同图形的面积计算公式:S三角形=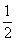 ×底×高,S平行四边形=底×高,S长方形=长×宽,S梯形=(上底+下底)×高×
×底×高,S平行四边形=底×高,S长方形=长×宽,S梯形=(上底+下底)×高×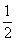 。因为两条平行线间的距离处处相等,所以所画图形的高都相等,题中要求所画图形的面积都与三角形ABC的面积相等,因此根据各图形的面积公式可推出:以平行线间的距离为高,平行四边形的底为4cm,长方形在平行线上的边的长度为4cm,梯形的上、下底之和为8cm。
。因为两条平行线间的距离处处相等,所以所画图形的高都相等,题中要求所画图形的面积都与三角形ABC的面积相等,因此根据各图形的面积公式可推出:以平行线间的距离为高,平行四边形的底为4cm,长方形在平行线上的边的长度为4cm,梯形的上、下底之和为8cm。
解答:画法不唯一,各种图形仅举一例。
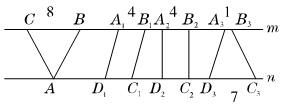
所画图形为平行四边形A1 B1 C1 D1,长方形A2 B2 C2 D2,梯形A3 B3 C3 D3。
第8题
∠2=90°-(180°-145°)=55°
第9题
情况一:顶角是50°。
(180°-50°)÷2=65°
另外两个内角都是65°。
情况二:一个底角是50°。
180°-50°×2=80°
另外两个内角分别是50°、80°。
第10题
分析:要使从M、N两村各挖的一条水渠最短,应从M、N两村各取一点,从这一点到河边所画的垂线段最短。
解答:
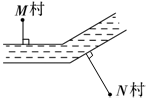
第11题
分析:在同一个平面内,如图①,过2个点最多能连成1条直线;如图②,过3个点最多能连成1+2=3(条)直线;如图③,过4个点最多能连成1+2+3=6(条)直线。根据以上规律,过5个点最多能连成1+2+3+4=10(条)直线;过6个点最多能连成1+2+3+4+5=15(条)直线;过9个点最多能连成1+2+3+4+5+6+7+8=36(条)直线。由此推出过100个点最多能连成1+2+3+4+…+99=4950(条)直线。
解答:
(1)4 10
(2)1+2+3+4+5 15 36
(3)1+2+3+4+…+99=4950(条)
(2)图形的认识与测量(二)
第1题
(1)4
(2)20.56
(3)45
(4)8
第2题
(1)B
(2)分析:在一个正方形内画一个最大的圆,圆的直径是正方形的边长,即d=a,
C圆=πd,C正方形=4a,圆的周长与正方形的周长之比为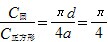 ,所以选B。
,所以选B。
解答: B
(3)C
(4)B
(5)分析:圆的周长大小与圆的直径大小有关。
①的周长为5π;
②的周长π×5×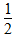 +π×2×
+π×2×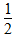 +π×3×
+π×3×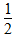 =5π;
=5π;
③的周长π×5×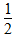 +π×3×
+π×3×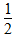 +π×2×
+π×2×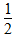 =5π;
=5π;
④的周长π×5×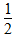 +π×1×
+π×1×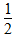 +π×4×
+π×4×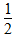 =5π,所以选C。
=5π,所以选C。
解答: C
第3题
(1)× (2)× (3)×
(4)√ (5)×
第4题
5 dm
第5题
分析:本题考查的是平面图形的面积计算。观察图形:长方形的长=平行四边形的高=圆的直径,可通过平行四边形的面积为24 cm2和底为4 cm,求出平行四边形的高为24÷4=6(cm),再求长方形的面积=长×宽=6×5=30(cm2),圆的面积=πr2=π(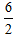 )2=3.14×(
)2=3.14×(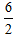 )2=28.26(cm2)
)2=28.26(cm2)
解答:
24÷4=6(cm)………………(2分)
S长方形:5×6=30(cm2)………………(2分)
S圆形: 3.14×(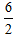 )2=28.26(cm2)…………(2分)
)2=28.26(cm2)…………(2分)
第6题
分析:本题考查的是学生计算平面图形的面积的能力。由图可知正方形的边长是圆的半径,正方形的面积为5 cm2,即a2=5,等同于圆的半径的平方,即r2=5,那么圆的面积为πr2=3.14×5=15.7(cm2)。
解答:
a=r  a2=r2=5………………(2分)
a2=r2=5………………(2分)
S=3.14×r2………………(2分)
=3.14×5
=15.7(cm2)……………………(2分)
第7题
(1)2826 m
(2)
①分析:本题考查的是学生的观察力。观察此图发现用半圆的面积减去直角三角形的面积,可得阴影部分的面积。直角三角形的两条直角边都是半圆的半径,即8÷2=4(cm),先求出三角形面积为4×4÷2=8(cm2),再求出半圆的面积为3.14×42×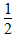 =25.12(cm2),最后求差,即25.12-8=17.12(cm2)。
=25.12(cm2),最后求差,即25.12-8=17.12(cm2)。
解答:
分步列式:
r:8÷2=4(cm)………………(1分)
S三角形:4×4÷2=8(cm2)………………(1分)
S半圆:3.14×42×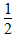 =25.12(cm2)…………………………(2分)
=25.12(cm2)…………………………(2分)
S阴影:25.12-8=17.12(cm2)………………(2分)
综合列式:
3.14×(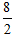 )2×
)2×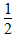 -(
-(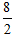 )×(
)×(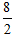 )÷2=17.12(cm2)…………(6分)
)÷2=17.12(cm2)…………(6分)
②分析:观察此图发现用梯形面积减去三角形面积,可得阴影部分的面积。根据已知数据,首先求出三角形的面积为3×4÷2=6(cm2),然后求出底边为5 cm时三角形的高为6×2÷5=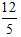 (cm)。这条高也是梯形的高,进而求出梯形的面积为(5+10)×
(cm)。这条高也是梯形的高,进而求出梯形的面积为(5+10)×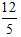 ÷2=18(cm2),最后求出图中阴影部分的面积为S阴影=S梯形-S三角形=18-6=12(cm2)
÷2=18(cm2),最后求出图中阴影部分的面积为S阴影=S梯形-S三角形=18-6=12(cm2)
解答:
分步列式:
3×4÷2=6(cm2)………(1分)
6×2÷5=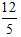 (cm)…………(2分)
(cm)…………(2分)
(5+10)×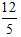 ÷2=18(cm2)………………(2分)
÷2=18(cm2)………………(2分)
18-6=12(cm2)……………………(1分)
综合列式:
(5+10)×(3×4÷2×2÷5)÷2-3×4÷2………………(3分)
=15×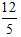 ÷2-12÷2
÷2-12÷2
=18-6
=12(cm2)………………(3分)
第8题
(1)分析:求建这个羊圈至少需要多长的栅栏就是求半圆的周长,即2πr÷2=2×3.14×5÷2=15.7(m)
解答:
3.14×5=15.7(m)…………(7分)
答:建这个羊圈至少需要15.7 m的栅栏。…………(1分)
(2)分析:实际上就是求直径增加2 m后半圆的面积比原来半圆的面积多多少。根据圆的面积的计算公式可求出现在半圆的面积为3.14×[(5×2+2)÷2]2÷2=56.52(m2)
原来半圆的面积为3.14×52÷2=39.25(m2)
增加的面积为56.52-39.25=17.27(m2)
解答:
3.14×[(5×2+2)÷2] 2÷2-3.14×52÷2…………(4分)
=3.14×62÷2-3.14×52÷2
=56.52-39.25
=17.27(m2)…………(3分)
答:羊圈的面积增加了17.27 m2。…………(1分)
第9题
分析:根据已知“圆的面积等于长方形的面积”可推出阴影部分的面积是圆面积的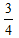 。又“已知圆的周长是25.12 cm”可推出圆的半径为25.12÷3.14÷2=4(cm)。可得出阴影部分面积为3.14×42×
。又“已知圆的周长是25.12 cm”可推出圆的半径为25.12÷3.14÷2=4(cm)。可得出阴影部分面积为3.14×42×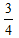 =37.68(cm2)
=37.68(cm2)
解答:
3.14×(25.12÷3.14÷2)2×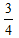 …………(5分)
…………(5分)
=3.14×42×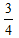
=37.68(cm2)…………(4分)
答:阴影部分的面积是37.68 cm2。…………(1分)
(3)图形的认识与测量(三)
第1题
(1)4
(2)圆锥 高 底面半径
第2题
(1)B (2)C
第3题
(1)√ (2)×
(3)√ (4)×
第4题
90 cm2 54 cm3
第5题
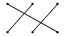
第6题
63÷10.8÷2.5=8(dm)
第7题
5×2×3=30(cm3)
第8题
(1)3.14×20×1.5+3.14×(20÷2)2=408.2(m2)
(2)3.14×(20÷2)2×1=314(m3)
第9题
(4×2+2×15)×2+3.14×(4÷2)2+3.14×4×15×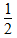 =182.76(m2)
=182.76(m2)
第10题
分析:(1)假设每个小正方体的体积为1,所以求大正方体共有多少个小正方体,就是求这个立体图形的体积,即33=27(个);求用这样的小正方体搭成一个大正方体至少需要几个,就是求当棱长为比1大的最小整数时,所需小正方体的个数,也就是当棱长为2时的正方体的体积,即23=8(个);无论从哪面看,都能看到边长为2的正方形,即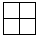 。
。
解答:
27………………(2分)
8…………………………(2分)
 ………………(2分)
………………(2分)
(2)分析:
①正方体的8个顶点上的小正方体被涂了三个面,所以有8个。
②原正方体的12条棱上除去顶点的排在中间的小正方体被涂了两个面,所以有12个。
③原正方体6个面中,每个面中间的小正方体,被涂了一个面,所以有6个。
④原正方体最中间的那块小正方体,没有涂黄色,所以只有1个。
解答:
①8………………(3分)
②12………………(3分)
③6………………(3分)
④1………………(3分)
第11题
方法一:
分析:瓶子正放和倒时的容积与酒精的体积不变,所以瓶子空余部分的容积相等。因此,酒精瓶的容积就相当第一幅图中酒精的体积加上第二幅图中空余部分的体积,即一个高为(6+2)cm的圆柱形容器的容积。先求容器的底面积:240÷6=40(cm2),再求酒精瓶的容积40×(6+2)=320(mL)。
解答:
240 mL=240 cm3
240÷6=40(cm2)………………(5分)
40×(6+2)=320(cm3)=320(mL)………………(4分)
方法二:假设瓶子的容积是x毫升,因瓶子的底面积一定,所以可用正比例知识解答,根据底面面积=容积÷高,列比例为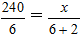 ,解得x=320。
,解得x=320。
解:设这个酒精瓶的容积是x毫升。………………(1分)
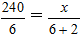 ………………(4分)
………………(4分)
x=320…………………………(4分)
答:这个酒精瓶的容积是320毫升。………………(1分)
