1.圆柱 - (4)圆柱的体积(一)
第1题
(1)高 底面积 底面积×高 底面积×高 V=Sh
(2)300
(3)6
(4)扩大到原来的3倍
第2题
(1)√ (2)× (3)×
(4)√ (5)× (6)×
第3题
(1)B (2)A
(3)B (4)C
第4题
3.14×(18÷2)2×15=3815.1(cm3)
第5题
(1)3.14×32×2.5×550=38857.5(kg)
38857.5 kg=38.8575 t
(2)8×6=48(dm2)
第6题
85 mm=8.5 cm
7 mm=0.7 cm
3.14×(8.5÷2)2×0.7≈40(cm3)
第7题
分析:本题考查了物体形状变化后体积不变的知识点。由长方体钢坯熔铸成圆柱体时,变化的是物体的形状,不变的是物体的体积,即V长方体=V圆柱,而V长方体=长×宽×高=31.4×20×4=2512(cm3),V圆柱=底面积×高。
解答:
熔铸前长方体的体积:
31.4×20×4……(3分)
=2512(cm3)……(1分)
熔铸后圆柱的高:
2512÷(3.14×42)……(2分)
=2512÷50.24
=50(cm)……(1分)
答:圆柱的高是50厘米。……(1分)
第8题
(1)
分析:钢管的体积=外圆柱的体积-内圆柱的体积。
解答:
(1)内圆柱的体积…………(1分)
(2)3.14×42×50 3.14×32×50 1099………(每空2分)
(3)方法一
分析:根据求圆柱的体积公式V圆柱=底面积×高=π×半径2×高,要先求出钢管底面内外圆的半径,然后计算内外圆柱的体积差,就是钢管的体积。
解答:10÷2=5(cm)………………(1分)
8÷2=4(cm)………………(1分)
3.14×52×50-3.14×42×50………………(2分)
=3.14×25×50-3.14×16×50
=3925-2512
=1413(cm3)………………(2分)
方法二
分析:先求钢管底面的环形面积,再求体积。
解答:
(3.14×52-3.14×42)×50………………(4分)
=3.14×9×50
=1413(cm3)………………(2分)
答:钢管的体积是1413 cm3。…………(1分)
第9题
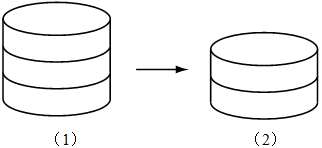
分析:本题考查了学生对圆柱表面积的掌握情况,及对圆柱体积公式的熟练应用情况。如图,由图(1)变成图(2),减少的面积就是一个小圆柱的侧面积,圆柱的侧面积=底面周长×高,所以 ,由此可求出一个小圆柱的高为314÷(3.14×2×10)=5(cm),然后求搭成的大圆柱的体积,体积=底面积×高,即3.14×102×5×3=4710(cm3)。
,由此可求出一个小圆柱的高为314÷(3.14×2×10)=5(cm),然后求搭成的大圆柱的体积,体积=底面积×高,即3.14×102×5×3=4710(cm3)。
解答:
一个小圆柱的高:
314÷(3.14×2×10)…………(2分)
=314÷62.8
=5(cm)………………(1分)
搭成的大圆柱的体积:
3.14×102×5×3………………(2分)
=3.14×100×5×3
=4710(cm3)…………………………(2分)
答:这个由3个小圆柱搭成的大圆柱的体积是4710 cm3。…(1分)
&http_url=https://taozhi.cn/phone_a/58649.htm&http_referer=&http_response_type=html&other_client_id=388f2c38-cdbe-4d7f-95c6-0e816119acef&page_title=%EF%BC%884%EF%BC%89%E5%9C%86%E6%9F%B1%E7%9A%84%E4%BD%93%E7%A7%AF%EF%BC%88%E4%B8%80%EF%BC%89&client_type=PC%E7%BD%91%E7%AB%99&br_screen_height=720&br_screen_width=1280&br_platform=Linux%20x86_64&br_app_name=Netscape&page_load_time=1028&con_user_open_id=undefined)
