专项全练全测 - 学习领域专项全练全测(三)统计与概率
第二题
49下 26下 72下 86下 71下 96下
第三题
2. 5月5日 29℃-17℃=12℃ 14℃-4℃=10℃
3.根据气温变化,及时增减衣物。(答案不唯一,合理即可)
第四题
1. 360
2. 90
第五题
分析:
1.求张敏一共掷中几环,用加法计算,把张敏的三次成绩加到一起,即4+5+6=15(环)。
2.求李娜一共掷中几环用同样的方法,即8+3+7=18(环)。
3.李丽想要获胜就要比李娜得分多,也就是李丽掷中的环数要大于18,李丽第一次掷中了10环,第二次掷中了0环,两次一共掷中了10+0=10(环),李丽第三次掷中的要比李丽和李娜现在相差的环数要大,现在相差18-10=8(环),李丽第三次掷中的数要大于8,题目要求至少掷中几环,那就是选择大于8中最小的数,就是至少掷中9环。
解答:
1.4+5+6=15(环)………(3分)
答:张敏一共掷中15环。………(1分)
2.8+3+7=18(环)…………(3分)
答:李娜一共掷中18环。………(1分)
3.18-10=8(环) 9>8 至少掷9环。………(3分)
答:第三次至少要掷中9环。………(1分)
第六题
1.4.5-3.8=0.7(元)
2.2.4+3.8=6.2(元)
第七题
3×2=6(种)
第八题
分析:
这是排列问题,要根据一定的规律来排,再计算出一共有多少种排法。李老师和甲、乙、丙、丁四位同学合影,李老师站在中间,位置固定可以不考虑老师,只看甲、乙、丙、丁四个人的位置就能找到答案。这四位同学的位置排列如下所示:
甲站在第一位,乙、丙、丁分别站在第二位,共有6种排列方法。(如下所示)

乙站在第一位,甲、丙、丁分别站在第二位,也有6种排列方法。(如下所示)
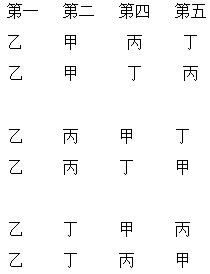
丙站在第一位,甲、乙、丁分别站在第二位,也有6种排列方法。(如下所示)
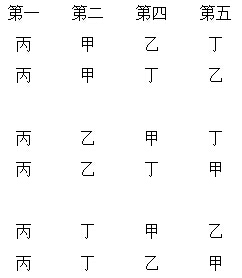
丁站在第一位,甲、乙、丙分别站在第二位,也有6种排列方法。(如下所示)
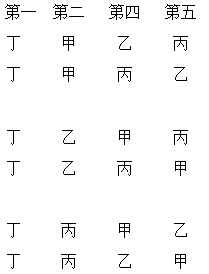
解答: 4×6=24(种)
答:一共有24种不同的站法。
