专项全练全测 - 学习领域专项全练全测(二)
第一题
1.0.75 6400 2.(1)立方厘米 (2)升(3)米 (4)平方厘米
3.4 96 4.16 8 5.64 6.120 7.0.5
第二题
1.√ 2.× 3.× 4.√ 5.√
第三题
1.B
2. 分析:根据从正面看到的图可知,这个立体图是由二层组成的,且底层至少有3个小正方体,上层至少有1个小正方体;根据从上面看到的图可知,这个立体图的底层是由4个小正方体组成的。要保证组成的立体图形用到的小正方体个数最少,那么底层的4个小正方体必不可少,而上层至少有一个小正方体。如图:
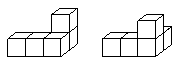
解答:C ……(2分)
3.B 4.B 5.C
6. 分析:根据“用4个表面积都是24平方米的正方体拼成一个模型”可知拼成这个模型的每个正方体的一个面的面积是24÷6=4(平方米);通过观察这个模型可知这个模型的表面积是由18个面积是4平方米的小正方形组成的。即18×4=72(平方米)。
解答:B ……(2分)
第四题
1.6×6×6=216(平方分米)
6×6×6=216(立方分米)
2.4.5×15×2+3.2×15×2+3.2×4.5×2=259.8(平方米)
3.2×4.5×15=216(立方米)
第六题
1.(1)4 3 3 3 (2)6 72
2.6×5=30(平方米)
6×5+6×4×2+5×4×2=118(平方米)
3.(13-2×2)×(9-2×2)×2=90(立方厘米)
4.5升=5立方分米
5÷(2×2)=1.25(分米)=12.5(厘米)
15-12.5=2.5(厘米) 2分米=20厘米
20×20×2.5=1000(立方厘米)
6.分析:(1)如果把长14厘米,宽9厘米,高4厘米的长方体截成体积最大的正方体,那么这个最大的正方体的棱长是这个长方体的高,即棱长为4厘米;其体积为4×4×4=64(立方厘米)
(2)根据截成体积最大的正方体的棱长为4厘米,看原来长方体的宽有几个正方体的棱长,即9÷4=2(个)……1(厘米);原来长方体的长有几个正方体的棱长,即14÷4=3(个)……2(厘米)。则这个长方体最多能截成2×3=6(个)这样的正方体。
解答:(1)4×4×4=64(立方厘米)……(2分)
(2)长方体的宽能截成正方体的棱长的个数:9÷4=2(个)……1(厘米)……(4分)
长方体的长能截成正方体的棱长的个数:14÷4=3(个)……2(厘米)……(6分)
长方体最多能截成2×3=6(个)这样的正方体。……(8分)
