1.图形的认识与测量 - （3）图形的认识与测量（三）
第1题
（1）4 （2）圆锥 高 底面半径
第2题
（1）B （2）C
第3题
（1）√ （2）× （3）√ （4）×
第4题
90 cm2 54 cm3
第5题
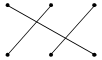
第6题
63÷10.8÷2.5＝8（dm）
第7题
5×2×3＝30（cm3）
第8题
1）3.14×20×1.5＋3.14×(20÷2)2＝408.2（m2）
（2）3.14×(20÷2)2×1＝314（m3）
第9题
3.14×42×8－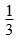
×3.14×42×(8－6)≈368（cm3）
第10题
1）分析：观图可知，图中共有3层小正方体，每层有9个小正方体，所以图中共有3×9＝27(个)小正方体。假设每个小正方体的体积为1，求用这样的小正方体搭一个大正方体至少需要几个，就是求当棱长为比1大的最小整数时，所需小正方体的个数，也就是求当棱长为2时的正方体的体积，即23＝8（个）。搭成的大正方体无论从哪面看，看到的都是边长为2的正方形，即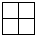
。
解答： 27…………（2分）
8…………（4分）
…………（6分）
（2）分析：①大正方体的8个顶点上的小正方体被涂了三个面，所以有8个。②大正方体的12条棱上除去顶点的排在中间的小正方体被涂了两个面，所以有12个。③大正方体的6个面中，每个面中间的小正方体被涂了一个面，所以有6个。④大正方体最中间的那块小正方体没有涂黄色，所以只有1个。
解答：①8…………（9分）
②12…………（12分）
③6…………（15分）
④1…………（18分）
第11题
分析：酒精瓶正放和倒放时的容积与酒精的体积不变，所以酒精瓶正放和倒放时空余部分的容积相等。因此，酒精瓶的容积就相当于一个高为（6＋3）cm的圆柱形容器的容积。
解答：240 mL＝240 cm3…………（2分）
240÷6＝40（cm2）…………（5分）
40×(6＋3)＝360(cm3)＝360(mL)…………（9分）
答：这个酒精瓶的容积是360 mL。………………（10分）