1.比例的意义和基本性质 - （2）比例的基本性质
第1题
（1）外 内 （2）9 4 12 3
第2题
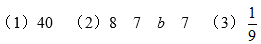
第3题
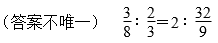
第4题
（1）分析：要使甲、乙两队的人数比为3∶2，在方案1和方案2中，当乙队人数不变时，说明每份人数为22÷2＝11（人），那么甲队就应有11×3＝33（人），而实际甲队只有28人，所以只能增加人数，不能减少人数，因此方案1不可行，方案2可行，应调33－28＝5（人）。在方案3和方案4中，当甲队人数不变时，每份人数（28÷3）不是自然数，所以这两种方案都不可行。方案5和方案6是保证总人数不变，调整两队人数，那么甲队应有（28＋22）÷（3＋2）×3＝30（人），乙队应有（28＋22）－30＝20（人），方案5中，甲队人数本已不足，无法再调到乙队，所以不可行，方案6可行，从乙队调22－20＝2（人）到甲队。
解答：
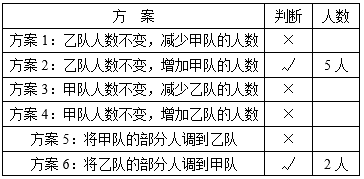
（2）分析：无论如何调整人数，都要遵循甲队人数÷3和乙队人数÷2的商相等，即每份人数相等。
解答：（答案不唯一）甲队：28－1＝27（人）…………（2分）
乙队：27÷3＝9（人） 22－（2×9）＝4（人）…………（4分）
甲队减少1人，乙队减少4人。…………（5分）
第5题
分析：本题考查的是比例的基本性质的运用及比例的各部分名称的掌握。根据在比例中，两个外项的积等于两个内项的积，可以用两个外项的积（或两个内项的积）除以一个内项（或外项），就可求出组成比例的另一个内项（或外项）是多少。
解答：（1）8×40÷32＝10…………（2分）
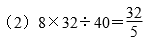…………（4分）
（3）40×32÷8＝160…………（6分）
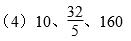…………（7分）
（5）8×40÷20＝16…………（9分）
8×20÷40＝4…………（11分）
20×40÷8＝100…………（12分）
这个数可以是16、4、100。…………（13分）