学霸易错题 - 第三单元 圆柱与圆锥
易错点1 对圆柱侧面展开图的形状认识不清
例1 判断：一个圆柱的侧面展开图只能是长方形或正方形。（ ）
错解 √
错因剖析 当圆柱的侧面沿圆柱的高展开时，其侧面展开图是一个长方形或正方形；当圆柱的侧面不沿圆柱的高展开时，其侧面展开图是其他形状的图形。
正确解答 ×
点拨 圆柱的侧面只有沿圆柱的高展开时，其侧面展开图才是长方形或正方形。
跟踪练习
1.圆柱侧面展开图不可能是下面的（ ）图形。
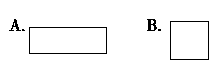
2.把一个圆柱的侧面沿高展开后得到一个正方形，那么它的底面直径和高相等。（ ）
答案 1.D 2.×
易错点2 特殊圆柱的表面积所指不明确
例2 压路机的滚筒是个圆柱，它的宽是2米，滚筒横截面的半径是0.6米，那么滚筒转一周可以压路多少平方米？
错解 3.14×0.6×2×2+3.14×0.62×2=9.7968（平方米）
答：滚筒转一周可以压路9.7968平方米。
错因剖析 压路机压路时是它的侧面与地面接触，所以应该求它的侧面积，与两个底面无关。
正确解答 3.14×0.6×2×2=7.536（平方米）
答：滚筒转一周可以压路7.536平方米。
点拨 求压路机、通风管、烟囱等特殊圆柱形物体的表面积时，其实就是求它们的侧面积。
跟踪练习
1.如下图，一台压路机的前轮宽1.6米，滚筒横截面的直径是0.8米，每分钟转18周。这辆压路机每分钟前进多少米？每分钟压过的路面有多大？
2.一顶圆柱形的厨师帽，高是3分米，帽顶周长是62.8分米，做这样一顶帽子至少需要多少面料？
答案 1.3.14×0.8×18=45.216（米） 3.14×0.8×1.6×18=72.3456（平方米）
2.62.8×3+3.14×（62.8÷3.14÷2）2=502.4（平方分米）
易错点3 求需要丝带的长度不能只算露在外面的
例3 小明生日那天，同学们送给他一个大蛋糕，蛋糕盒是一个圆柱，服务员阿姨说要配上十字形的丝带才漂亮，你知道要买多长的丝带吗？（蝴蝶结需要20厘米）
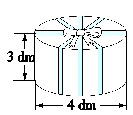
错解 20厘米=2分米 3×3+4×4+2=27（分米）
错因剖析 此题错在只是计算了丝带露在外面的长度，实际上还包括下面4条直径的长度和侧面5条高的长度，再与蝴蝶结需要的20厘米加在一起才是需要丝带的长度。
正确解答 20厘米=2分米 3×8+4×8+2=58（分米）
答：要买58分米长的丝带。
点拨 在解答这类题时，要注意观察，认真审题，把所用的材料求完整。
跟踪练习
1.一个圆柱形蛋糕包装盒的底面直径是40cm，高是10cm，用彩带将它捆扎起来（如下图），打结处在圆心，且彩带长30cm。一共用去彩带多少厘米？
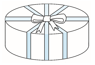
2.一个礼品盒用彩带扎成了下面的形状，打结处用去彩带25cm，包装这个礼品盒一共用去彩带多少厘米？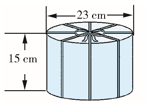
答案 1.40×8+10×8+30=430（cm） 2.（23+15）×8+25=329（cm）
易错点4 会求圆柱的体积，却不知道体积的变化规律
例4 判断：圆柱的底面半径扩大到原来的2倍，高缩小到原来的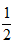
，它的体积不变。（ ）
错解 √
错因剖析 圆柱的体积是由它的底面积和高决定的。底面半径扩大到原来的2倍，底面积扩大到原来的4倍，高缩小到原来的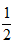，就相当于圆柱的体积扩大到原来的2倍。
点拨 圆柱的体积是由底面积和高决定的，解题时要综合考虑，不能片面下结论。
跟踪练习
1.圆柱的体积不变，如果底面半径扩大到原来的2倍，高应该（ ）。
A.扩大到原来的2倍 B.缩小到原来的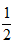
C.缩小到原来的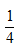
D.扩大到原来的4倍
2.圆柱的底面积缩小到原来的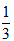
，高扩大到原来的2倍，它的体积（ ）。
A.扩大到原来的6倍 B.缩小到原来的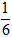
C.缩小到原来的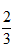
D.扩大1.5倍
答案 1.C 2.C
易错点5 计算圆锥的体积时忘记乘“”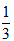
例11 有一个圆锥形沙堆，底面周长是12.56m,高是0.9m，用这堆沙在宽6m的长方形路上铺2cm厚的路面，能铺多少米？
错解 2cm=0.02m 3.14×（12.56÷3.14÷2）2×0.9÷6÷0.02=94.2（m）
答：能铺94.2m。
错因剖析 把圆锥形沙堆的沙子铺在长方形路上，体积不变，但在求圆锥的体积时只是用底面积乘高而没有乘“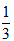”，另外还要注意统一单位。
正确解答 2cm=0.02m
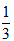×3.14×（12.56÷3.14÷2）2×0.9÷6÷0.02=31.4（m）
答：能铺31.4m。
点拨 圆锥的体积是与它等底等高的圆柱体积的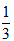，所以在计算圆锥的体积时不要忘记乘“”。
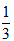跟踪练习
1.一个圆锥形沙堆，底面积是37.68平方米，高是3米。用这堆沙在10米宽的长方形公路上铺3厘米厚的路面，能铺多少米？
2.一个圆锥形沙堆，底面周长是25.12m，高是3m，现在把它铺在5m宽的路上能铺20cm厚，铺了多长的一段路？
答案 1.37.68×3×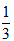÷10÷（3÷100）=125.6（m）
2.3.14×（25.12÷3.14÷2）2×3×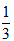÷5÷（20÷100）=50.24（m）
易错点6 对圆柱表面积的概念理解不准确
例6 如图，求半圆柱的表面积。（单位：cm）
错解 [3.14×6×4+3.14×（6÷2）2×2]÷2=65.94（cm2）
答：半圆柱的表面积是65.94 cm2。
错因剖析 此题错在没有准确掌握圆柱表面积的概念，错误地认为半圆柱的表面积等于圆柱的表面积除以2。计算半圆柱的表面积时，除了用表面积除以2外，还要加上截面的长方形的面积。
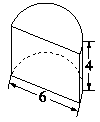
正确解答 [3.14×6×4+3.14×（6÷2）2×2]÷2+6×4=89.94（cm2）
答：半圆柱的面积是89.94 cm2。
点拨 在计算特殊圆柱的表面积时，要先看清这个图形包含哪些面的面积，再解答。
跟踪练习
1.求出下面图形的表面积。
2.将一根1米长的圆木沿着直径劈成相等的两半，表面积增加了1.8平方米。原来这根圆木的表面积是多少？
答案 1.3.14×8×12÷2+3.14×（8÷2）2+12×8=296.96（平方厘米）
2.1.8÷2÷1×3.14×1+3.14×（1.8÷2÷1÷2）2×2=4.0977（平方米）
易错点7 有关圆柱和圆锥的关系问题记不清
例7 一个圆柱形鱼缸，底面直径是40cm，高是25cm,里面盛了一些水，把一个底面半径为10cm的圆锥放入鱼缸中（圆锥全部浸入水中），鱼缸中的水面升高了2cm。这个圆锥的高是多少？
错解 3.14×（40÷2）2×2÷（3.14×102）=8（cm）
答：这个圆锥的高是8cm。
错因剖析 此题错在没有正确利用圆锥的体积计算公式，把圆锥放入鱼缸中，水面升高2cm的那段水柱的体积就是圆锥的体积，在知道体积和底面积求高时，用体积除以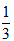，再除以底面积就可求出圆锥的高。
正确解答 3.14×（40÷2）2×2÷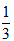÷（3.14×102）=24（cm）
答：这个圆锥的高是24cm。
点拨 鱼缸中水面升高那段水柱的体积就是放入水中圆锥的体积。
跟踪练习
1.在一个直径是20cm的圆柱形容器里，放入一个底面半径是3cm的圆锥形铁块，全部浸入水中，这时水面上升0.3cm。圆锥形铁块的高是多少厘米？
2.把一个圆柱削成一个最大的圆锥，削去部分的体积为40立方厘米，求原来圆柱的体积。
答案 1.3.14×（20÷2）2×0.3÷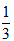÷（3.14×32）=10（cm )
2.40÷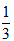=60（立方厘米）