1.认识三角形(19) - (2)三角形三边的关系及内角和
第一题
(1)△ (3)△ (4)△
第二题
(1)× (2)×
第四题
(1)100° (2)50° (3)25°
第五题
 三角形的内角和是180°
三角形的内角和是180°
第六题
第七题
(1)分析:根据平角是180°,如图,可知∠1=180°-70°=110°;又根据三角形的内角和是180°,可得∠?=180°-110°-35°=35°。
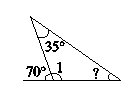
解答:∠?=180°-110°-35°=35°……(6分)
(2)分析:三角形中有一个角是直角,那么由三角形的内角和是180°可知,另外两个内角的和是90°,所以另外两个内角一定都是锐角。
由另外两个角的度数差是20°,根据两个数的和差公式:(和+差)÷2=较大数,(和-差)÷2=较小数,可求出其中较大角为(90°+20°)÷2=55°,较小角为(90°-20°)÷2=35°。
解答:(90°+20°)÷2 ……(2分)
=110°÷2
=55° ……(1分)
(90°-20°)÷2 ……(2分)
=70°÷2
=35° ……(1分)
第八题
3条 走第②条最近。
第九题
(1)7米 47米 (2)15°
第十题
(1)180° 2 360°
(2)180°×2=360°或180°+180°=360°
(3)分析:
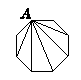
如图所示由正八边形的一个顶点A向不相邻的其他顶点连线,可以把正八边形分成6个三角形,所以正八边形的内角和与6个三角形的内角总和相等。
解答:180°×6=1080°
