六年级数学(上册) - 五 圆
1.圆的认识
第1题
( △ ) ( ) ( )
第3题
(1)B (2)C (3)A (4)C
第4题
(1)无数 相等 一半
(2) 4
(3) 6 3
(4) 2:1
第7题
分析:要在一个长为10㎝,宽为8㎝的长方形彩纸内剪半径为2cm的圆,就是看长和宽各有多少个直径,因为半径是2㎝,所以直径是4厘米,因为8÷4=2,所以宽中有2个直径,因为10÷4=2……2,所以长中有2个直径,所以最多能剪2×2=4(个)圆。
解答:2×2=4(cm)……(2分)
8÷4=2(宽中有2个直径)……(4分)
10÷4=2……2(长中有2个直径)……(6分)
2×2=4(个)……(7分)
答:最多能剪4个半径是2cm的圆。……(8分)
第8题
分析:题中长方形的宽是3㎝,也就是圆的直径是3㎝,而长方形的长相当于3个圆的直径,所以长方形的长为3×3=9(㎝),所以长方形的面积=长×宽=(3×3)×3=27(㎝²)。
解答:分步列式:
3×3=9(㎝)……(4分)
9×3=27(㎝²)……(7分)
答:这个长方形的面积是27㎝²。……(8分)
综合列式:
(3×3)×3=27(㎝²)……(7分)
答:这个长方形的面积是27㎝²。……(8分)
第9题
(1)A(3,3) B(5,8) C(8,4)
(2)下 4 右 3(或右 3 下 4)
第10题
分析:本题主要考查学生的画图能力以及分析能力。3条直线最多把圆分成几部分,要分的最多,这3条直线就要两两相交,交点不重合且在圆内,如左下图所示,最多把圆分成7部分。同理4条直线时,每条直线都与其他3条直线相交,每两条直线的交点都不重合且在圆内,如右下图所示,最多把圆分成11部分。

解答:7部分……(4分)
11部分……(8分)
2.圆的周长
第2题
(1)× (2)× (3)× (4)√
第3题
(1)9.42 cm (2)21.98 dm
第4题
(1)A (2)A (3)A (4)C (5)A
第5题
2×3.14×2.75=17.27(m)
第6题

第7题
2.4×3.14=7.536(m)
【※浙江专用】10×3.4=31.4(m)
第8题
(6-0.348)÷3÷(3.14×2)=0.3(m)
第9题
2260.8÷(3.14×0.6×100)=12(分)
第10题
分析:本题考查圆周长的计算公式及应用。如图所示: ,把绳子的长分成三部分,一部分是弧形正好拼成一个半径为5㎝的圆,另一部分正好是4个直径,最后一部分是绳子接头部分。所以绳子的长为2×3.14×5+5×2×4+20=91.4(㎝)。
,把绳子的长分成三部分,一部分是弧形正好拼成一个半径为5㎝的圆,另一部分正好是4个直径,最后一部分是绳子接头部分。所以绳子的长为2×3.14×5+5×2×4+20=91.4(㎝)。
解答:分步列式:
2×3.14×5=31.4(㎝)……(3分)
5×2×4=40(㎝)……(5分)
31.4+40+20=91.4(㎝)……(7分)
答:一共需要绳子91.4cm。……(8分)
综合列式:
2×3.14×5+5×2×4+20=91.4(cm)……(7分)
答:一共需要绳子91.4cm。……(8分)
第11题
3.14×17.5÷1.7≈33(个)
第12题
分析:如图所示: 因为第一条小虫沿大半圆爬行,所以路程=大圆周长的一半=3.14×(3+2+1)÷2=9.42(cm);因为第二条小虫沿三个小半圆爬行,所以路程=三个小圆周长的一半=(3.14×3+3.14×2+3.14×1)÷2=9.42(cm)。9.42cm=9.42cm,路程相同,速度相同,根据时间=路程÷速度,所用时间也相同,所以两条小虫同时到达B地。
因为第一条小虫沿大半圆爬行,所以路程=大圆周长的一半=3.14×(3+2+1)÷2=9.42(cm);因为第二条小虫沿三个小半圆爬行,所以路程=三个小圆周长的一半=(3.14×3+3.14×2+3.14×1)÷2=9.42(cm)。9.42cm=9.42cm,路程相同,速度相同,根据时间=路程÷速度,所用时间也相同,所以两条小虫同时到达B地。
解答:第一条小虫:3.14×(3+2+1)÷2=9.42(cm)……(3分)
第二条小虫:(3.14×3+3.14×2+3.14×1)÷2=9.42(cm)……(6分)
9.42 cm=9.42 cm……(7分)
用相同的速度完成相同的路程所需的时间也相同,所以两条小虫同时到达B地。……(10分)
3.圆的面积(1)认识圆的面积
第1题
(1)× (2)× (3)√
第2题
(1)50.24 cm2 (2)28.26 cm2 (3)12.56 m2
第3题
3.14×52=78.5(cm2)
第4题
3.14×(8÷2)2=50.24(m2)
第5题
50.24÷3.14=16(m) 16÷2=8(m) 3.14×82=200.96(m2)
第6题
(1)C (2)B (3)A (4)C
第7题
3.14×(5-0.5)2=63.585(m2)
第8题
3.14×(65÷2)2=3316.625(m2)
65×3.14=204.1(m)
第9题
分析:本题考查圆的面积的计算公式。圆的面积=πr²,图中正方形的面积是20㎝²,因为正方形的边长是圆的半径,所以r²=20㎝²,所以圆的面积=πr²=3.14×20=62.8(㎝²)。
解答:3.14×20=62.8(㎝²)……(7分)
答:圆的面积是62.8㎝²。……(8分)
第10题
157÷(3.14×102)= 60×
60× =30(分)
=30(分)
第11题
分析:圆的面积=πr²,如图所示: 将圆中阴影部分进行转换。阴影部分的面积=
将圆中阴影部分进行转换。阴影部分的面积= 圆的面积-
圆的面积- 正方形的面积=3.14×2²×
正方形的面积=3.14×2²× -2×2×
-2×2× =1.14(㎝²)。
=1.14(㎝²)。
解答:分步列式:
3.14×2²× =3.14(㎝²)……(3分)
=3.14(㎝²)……(3分)
2×2× =2(㎝²)……(5分)
=2(㎝²)……(5分)
3.14-2=1.14(㎝²)……(7分)
答:阴影部分的面积是1.14㎝²。……(8分)
综合列式:
3.14×2²× -2×2×
-2×2× =1.14(㎝²)……(7分)
=1.14(㎝²)……(7分)
答:阴影部分的面积是1.14㎝²。……(8分)
第12题
分析:因为铁丝的长都是6.28m,所以小明围成的正方形的边长=6.28÷4=1.57(m),正方形的面积=1.57×1.57=2.4649(m²);小光围成的圆的半径=6.28÷3.14÷2=1(m),圆的面积=3.14×1²=3.14(m²),3.14>2.4649,所以小光围成的图形的面积大。
解答:分步列式:
6.28÷4=1.57(m)……(1分)
1.57×1.57=2.4649(m²)……(3分)
6.28÷3.14÷2=1(m)……(4分)
3.14×1²=3.14(m²)……(7分)
3.14>2.4649……(8分)
小光围成的图形的面积大。……(9分)
综合列式:
(6.28÷4)²=2.4649(m²)……(3分)
3.14×(6.28÷3.14÷2)²=3.14(m²)……(7分)
3.14>2.4649……(8分)
小光围成的图形的面积大。……(9分)
3.圆的面积(2)环形的面积
第1题
(1)3.14×132-3.14×102=216.66(cm2)
(2)3.14×(0.4+0.5)2-3.14×0.42=2.041(dm2)
(3)3.14×(31.4÷3.14÷2)2-3.14×22=65.94(cm2)
第2题
分析:本题考查圆环的概念及圆环面积的计算方法。圆环的概念是在一个大圆内剪去一个同心的小圆,剩下的部分就是圆环。圆环的面积等于外圆的面积与内圆面积的差。所以(1)√,(2)×。
解答:(1)√……(4分)(2)×……(8分)
第3题
(1)B (2)A
第4题
3.14×52-3.14×0.52=77.715(cm2)
第5题
12.56÷3.14÷2=2(m)
3.14×(2+1)2-3.14×22=15.7(m2)
第6题
分析:圆环的面积等于外圆的面积与内圆面积的差。阴影部分的面积=R²-r²=50(m²),圆环的面积=外圆的面积-内圆的面积=3.14×R²-3.14×r²=3.14×(R²-r²)=3.14×50=157(m²)。
解答:阴影部分的面积=R²-r²=50(m²)……(3分)
圆环的面积=3.14×R²-3.14×r²……(5分)
=3.14×(R²-r²)……(6分)
=3.14×50……(7分)
=157(m²)……(8分)
答:圆环的面积是157m²。……(9分)
3.圆的面积(3)解决问题
第1题
提示:分别以正方形的边长和长方形的宽作为直径画圆。
第2题
(1)102-3.14×(10÷2)2=21.5(cm2)
(2)102-3.14×(10÷2)2=21.5(cm2)
第3题

发现:在正方形内画一个最大的圆,圆的面积是正方形面积的 。
。
第4题
分析:在一个直径是6㎝的圆中剪一个最大的正方形,如图所示: ,圆的直径正好是正方形的对角线,如图把正方形分成两个直角三角形,这个正方形的面积=两个直角三角形面积的和=6×(6÷2)÷2×2=18(㎝²);剪去的部分的面积等于圆的面积与正方形的面积的差,即3.14×(6÷2)²-18=10.26(㎝²)。
,圆的直径正好是正方形的对角线,如图把正方形分成两个直角三角形,这个正方形的面积=两个直角三角形面积的和=6×(6÷2)÷2×2=18(㎝²);剪去的部分的面积等于圆的面积与正方形的面积的差,即3.14×(6÷2)²-18=10.26(㎝²)。
解答:
(1)6×(6÷2)÷2×2=18(㎝²)……………(3分)
答:这个正方形的面积是18㎝²……………………(4分)
(2)3.14×(6÷2)²-18=10.26(㎝²)………(7分)
答:剪去部分的面积是10.26㎝²。…………………(8分)
第5题
分析:可以先求出一半阴影部分的面积,如图所示: ,这一半阴影部分的面积=
,这一半阴影部分的面积=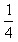 圆的面积-
圆的面积- 正方形的面积=3.14×10²×
正方形的面积=3.14×10²×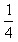 -10×10×
-10×10× =28.5(m²),所以阴影部分的面积=(
=28.5(m²),所以阴影部分的面积=(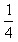 圆的面积-
圆的面积- 正方形的面积)×2=(3.14×10²×
正方形的面积)×2=(3.14×10²×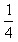 -10×10×
-10×10× )×2=57(m²)。
)×2=57(m²)。
解答:(3.14×10²×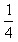 -10×10×
-10×10× )×2=57(m²)………(7分)
)×2=57(m²)………(7分)
答:两只羊都能吃到的草的面积是57平方米。………………(9分)
4.扇 形
第1题
× × √ × √ √
第2题
(1) (2)
(2)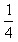 (3)圆心 (4)轴对称 1
(3)圆心 (4)轴对称 1
第3题
分析:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。(1)半圆是半个圆和经过这半个圆两端的两条半径所围成的图形是扇形。(2)扇形的面积不一定比圆的小,如一个大的扇形和一个小圆。(3)画扇形时,只要确定弧、弧的两端、圆心就可以画扇形了。
解答:√ × ×…………………(9分)
第5题
分析:先画一个半径为2㎝的圆,如图所示: 。
。
取圆上任意一点画半径,如图所示: 。
。
以圆心为顶点,用量角器画出30°的角,与圆交于另一点,即为所求,如图所示: 。
。
一个圆的圆心角为360°,360÷30=12(个),所以用12个这样的扇形可以拼成一个圆。
解答:画一个半径为2㎝的圆,如图所示: 。……(1分)
。……(1分)
取圆上任意一点画半径,如图所示: 。…………(2分)
。…………(2分)
以圆心为顶点,用量角器画出30°的角,与圆交于另一点,即为所求,如图所示: 。………(4分)
。………(4分)
360÷30=12(个)………(6分)
12个这样的扇形可以拼成一个圆。………(9分)
综合应用:确定起跑线
第1题
(1)85.96 72.6 75.1 77.6
第3题
分析:本题考查学生对椭圆式跑道结构的了解。要在标准的400m跑道上跑200m,一定会经过一个完整的半圆形跑道,所以只要求出在这个跑道上会相差几米就可以了,即π(R-r)。因为每条跑道宽1.25m,所以 R-r=1.25(m),相邻跑道中两人之间的起跑位置大约相差π(R-r)=3.14×1.25=3.925(m)。
解答:因为每条跑道宽1.25m,所以 R-r=1.25(m)。………(5分)
π(R-r)=3.14×1.25=3.925(m)………………………(6分)
答:相邻跑道中两人的起跑位置大约相差3.925m。……………(7分)
