六年级数学(上册) - 三 分数除法
1.倒数的认识
第1题
(1)倒数 倒数 (2)乘积
第2题
(1)C (2)B (3)A
第3题
(1)7  8 (2)0 1
8 (2)0 1
第4题
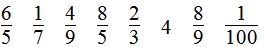
第5题
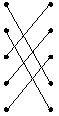
第6题
(1)× (2)× (3)√ (4)√ (5)×
第7题
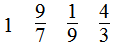
第8题
分析:本题考查的是倒数的性质。举例:当a=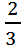 时,a的倒数是
时,a的倒数是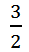 ,当a=
,当a=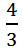 时,a的倒数是
时,a的倒数是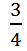 ;当a=1时,a的倒数是1。所以当a大于0且小于1时,a的倒数一定大于a;当a大于1时,a的倒数一定小于a;当a等于1时,a的倒数一定等于a。
;当a=1时,a的倒数是1。所以当a大于0且小于1时,a的倒数一定大于a;当a大于1时,a的倒数一定小于a;当a等于1时,a的倒数一定等于a。
解答:
(1)a大于0且小于1 ……(2分)
(2)大于1 ……(4分)
(3)等于1 ……(6分)
第9题
分析:两个数相乘,其中一个因数等于积乘另一个因数的倒数。本题中由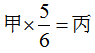 ,可推出甲=丙×
,可推出甲=丙×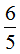 ,所以丙<甲;由乙×
,所以丙<甲;由乙×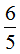 =丙,可推出乙=丙×
=丙,可推出乙=丙×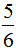 ,所以丙>乙。
,所以丙>乙。
解答:
乙<丙<甲 ……(5分)
第10题
分析:(1)一个数的倒数在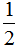 和
和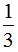 之间,在
之间,在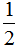 和
和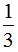 之间的数有无数个,如
之间的数有无数个,如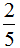 ,
,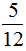 ,…写出其中一个,取其倒数即为所求。(2)一个自然数与它的倒数的和是5.2,这个自然数的倒数一定小于1,所以这个自然数的倒数为0.2,得出这个自然数是5。
,…写出其中一个,取其倒数即为所求。(2)一个自然数与它的倒数的和是5.2,这个自然数的倒数一定小于1,所以这个自然数的倒数为0.2,得出这个自然数是5。
解答:
(1)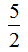 (答案不唯一) ……(6分)
(答案不唯一) ……(6分)
(2)5 ……(12分)
第11题
分析:本题考查的是倒数的意义。乘积是1的两个数互为倒数。所以互为倒数的两个数乘积是1。因为a、b互为倒数,所以ab=1。那么(1)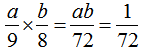 ;(2)
;(2)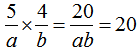 ,
,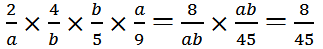 。
。
解答:
(1)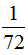 ……(2分)
……(2分)
(2)20 ……(4分)
(3)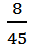 ……(6分)
……(6分)
第12题
分析:因为两个连续奇数的倒数的差是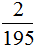 ,分母是195,所以这两个连续奇数的最小公倍数是195,先把195分解质因数,即195=3×5×13,且3×5×13=15×13,由此可以初步判定这两个连续奇数分别是13和15。用
,分母是195,所以这两个连续奇数的最小公倍数是195,先把195分解质因数,即195=3×5×13,且3×5×13=15×13,由此可以初步判定这两个连续奇数分别是13和15。用 进行验证,结果等于
进行验证,结果等于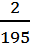 ,所以判定这两个连续的奇数是13和15。同理,当两个连续奇数的倒数的差是
,所以判定这两个连续的奇数是13和15。同理,当两个连续奇数的倒数的差是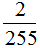 ,分母是255,所以这两个连续奇数的最小公倍数是255,先把255分解质因数,即255=3×5×17,且3×5×17=15×17,所以这两个连续的奇数是15和17。
,分母是255,所以这两个连续奇数的最小公倍数是255,先把255分解质因数,即255=3×5×17,且3×5×17=15×17,所以这两个连续的奇数是15和17。
解答:
(1)13 15 ……(4分)
(2)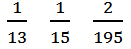 13 15 ……(14分)
13 15 ……(14分)
(3)15和17 ……(18分)
(1)分数除法的认识
第1题
(1)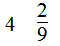
(2)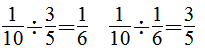
(3)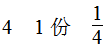
第2题
(1)× 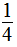
(2)÷ 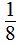
(3)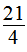 ×
×
(4)× 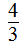
第3题
< < > > = = 小于 大于 等于
第4题
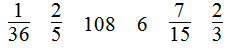
第5题
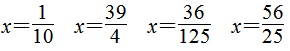
第6题
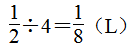
第7题
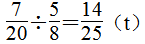
第8题
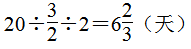
 ,这些药不够服一周。
,这些药不够服一周。
第9题
分析:本题考查分数除法的意义及计算方法。根据题意可知,一个数乘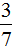 等于
等于 ,所以这个数=
,所以这个数= ÷
÷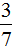 =
= ×
×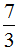 =
=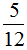 ,所以这道题正确的算法是
,所以这道题正确的算法是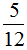 ÷
÷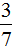 =
=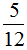 ×
×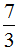 =
=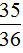 。
。
解答:
 ÷
÷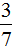 =
= ×
×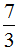 =
=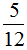 ……(3分)
……(3分)
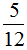 ÷
÷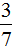 =
=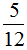 ×
×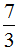 =
=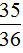 ……(6分)
……(6分)
第10题
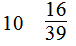
第11题
分析:当除法中除数或被除数是带分数时,要将带分数变成假分数再进行计算。本题中除数是带分数,所以将除数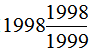 变成假分数
变成假分数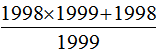 ,一个数除以假分数等于乘假分数的倒数,即乘
,一个数除以假分数等于乘假分数的倒数,即乘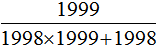 。
。
解答:
(1)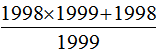 ……(2分)
……(2分)
(2) 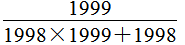
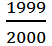 ……(6分)
……(6分)
(3)
原式=1998÷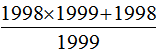
=1998×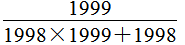 ……(8分)
……(8分)
=1998×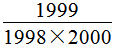
=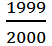 ……(10分)
……(10分)
(4)
原式=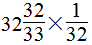
=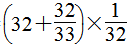 ……(12分)
……(12分)
=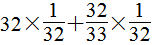
=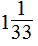 ……(14分)
……(14分)
(2)分数除法的混合运算
第1题
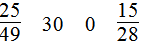
第2题
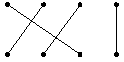
第3题
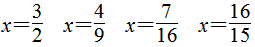
第4题
(1)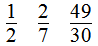
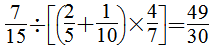
(2)
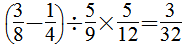
第5题
(1)A (2)B
第6题
分析:本题考查分数除法混合运算的简便运算。在计算分数除法混合运算时要将除法转化成乘法,再进行简便运算。本题主要运用乘法分配律进行简便运算,计算时要注意混合运算的运算顺序。
解答:
(1)
原式=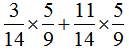 ……(1分)
……(1分)
=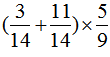 ……(2分)
……(2分)
=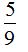 ……(3分)
……(3分)
(2)
原式=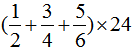 ……(4分)
……(4分)
=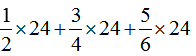
=12+18+20 ……(5分)
=50 ……(6分)
(3)
原式=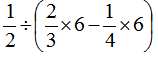 ……(7分)
……(7分)
=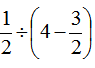
=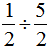
=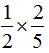 ……(8分)
……(8分)
=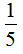 ……(9分)
……(9分)
(4)
原式=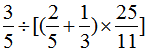
=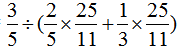 ……(10分)
……(10分)
=
=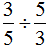 ……(11分)
……(11分)
=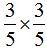
=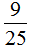 ……(12分)
……(12分)
第7题
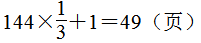
第8题
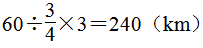
第9题
(1)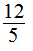 (2)
(2)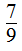
第10题
分析:乘积是1的两个数互为倒数。所以互为倒数的两个数乘积是1。因为a和b互为倒数,所以ab=1。根据“除以一个不为0的数等于乘这个数的倒数”解题。
解答:
(1)
原式=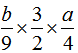 ……(1分)
……(1分)
=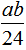 ……(2分)
……(2分)
=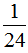 ……(4分)
……(4分)
(2)
原式= ……(5分)
……(5分)
=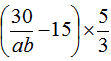 ……(6分)
……(6分)
=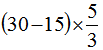 ……(7分)
……(7分)
=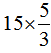
=25 ……(8分)
第11题
分析:红球比黄球少30个,每种球各增加1个后,红球还是比黄球少30个,但红球恰好是黄球的 ,所以红球比黄球少
,所以红球比黄球少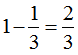 ,30和
,30和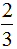 是对应关系,所以黄球有30÷
是对应关系,所以黄球有30÷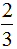 =45(个),原来黄球有45-1=44(个);原来红球有44-30=14(个)或45÷3-1=14(个)。
=45(个),原来黄球有45-1=44(个);原来红球有44-30=14(个)或45÷3-1=14(个)。
解答:
分步列式:
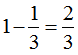 ……(2分)
……(2分)
30÷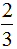 =45(个) ……(6分)
=45(个) ……(6分)
45-1=44(个) ……(8分)
44-30=14(个)或45÷3-1=14(个) ……(10分)
答:红球原来有14个,黄球原来有44个。 ……(12分)
综合列式:
30÷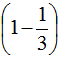 =45(个) ……(4分)
=45(个) ……(4分)
45-1=44(个) ……(6分)
44-30=14(个)或45÷3-1=14(个) ……(10分)
答:红球原来有14个,黄球原来有44个。 ……(12分)
(3)解决问题(1)
第1题
(1)全校学生人数
(2)公路的全长
(3)鸭的只数
第2题
分析:本题要求根据题意列出等量关系式。求一个数的几分之几是多少,用乘法计算。(1)全班人数的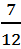 是男生,所以全班人数×
是男生,所以全班人数×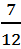 =男生人数;(2)桃树棵数是梨树棵数的
=男生人数;(2)桃树棵数是梨树棵数的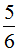 ,所以桃树棵数=梨树棵数×
,所以桃树棵数=梨树棵数×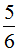 。
。
解答:
(1)全班人数×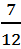 =男生人数 ……(5分)
=男生人数 ……(5分)
(2)梨树棵数×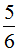 =桃树棵数 ……(10分)
=桃树棵数 ……(10分)
第3题
(1)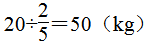
(2)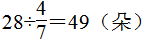
第4题
(1)解:设这座金字塔刚建成时的高度大约是x m。

(2)解:设解答太空知识用了x秒。
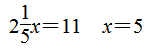
第5题
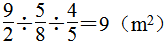
第6题
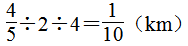
第7题
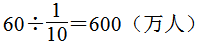
第8题
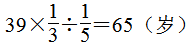
第9题
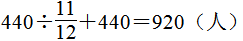
第10题
方法一
分析:由题可知,小明第一天看了全书的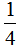 ,第二天看了全书的
,第二天看了全书的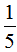 ,即第一天比第二天多看了全书的
,即第一天比第二天多看了全书的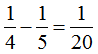 。又因为第一天比第二天多看了10页,10与
。又因为第一天比第二天多看了10页,10与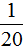 是对应关系,所以这本故事书一共有10÷
是对应关系,所以这本故事书一共有10÷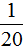 =200(页)。
=200(页)。
解答:
分步列式:
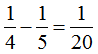 ……(5分)
……(5分)
10÷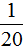 =200(页) ……(9分)
=200(页) ……(9分)
答:这本故事书一共有200页。 ……(10分)
综合列式:
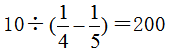 (页) ……(9分)
(页) ……(9分)
答:这本故事书一共有200页。 ……(10分)
方法二
分析:此题要求列方程解答。可设这本故事书一共有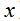 页,则第一天看了
页,则第一天看了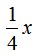 页,第二天看了
页,第二天看了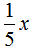 页,所以第一天比第二天多看了
页,所以第一天比第二天多看了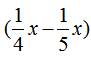 页,可列方程为
页,可列方程为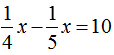 ,
,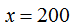 。
。
解答:
解:设这本故事书一共有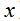 页。 ………(1分)
页。 ………(1分)
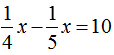 ……(5分)
……(5分)
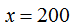 ……(9分)
……(9分)
答:这本故事书一共有200页。 ……(10分)
(4)解决问题(2)
第1题
(1)计划用煤量 计划用煤量 实际用煤量
(2)苹果的质量 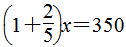
第2题
(1)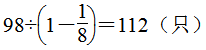
(2)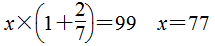
第3题
(1)× (2)√
第4题
(1)B (2)A
第5题
分析:根据题意可知,黑兔有20只,求白兔的只数。已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
(1)黑兔是白兔的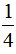 ,所以白兔的只数是黑兔的只数除以
,所以白兔的只数是黑兔的只数除以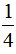 ,即
,即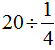 ;
;
(2)白兔是黑兔的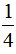 ,所以白兔的只数是黑兔的只数的
,所以白兔的只数是黑兔的只数的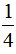 ,即
,即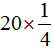 ;
;
(3)白兔比黑兔多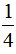 ,所以白兔的只数是黑兔的只数的
,所以白兔的只数是黑兔的只数的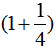 倍,即
倍,即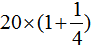 ;
;
(4)黑兔比白兔多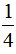 ,所以白兔的只数是黑兔的只数除以
,所以白兔的只数是黑兔的只数除以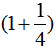 ,即
,即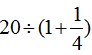 ;
;
(5)白兔比黑兔少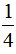 ,所以白兔的只数是黑兔的只数的
,所以白兔的只数是黑兔的只数的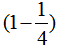 倍,即
倍,即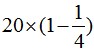 ;
;
(6)黑兔比白兔少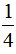 ,所以白兔的只数是黑兔的只数除以
,所以白兔的只数是黑兔的只数除以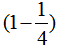 ,即
,即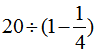 。
。
解答:
 ……(12分)
……(12分)
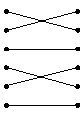
第6题
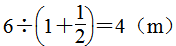
第7题
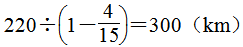
第8题
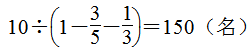
第9题
分析:根据题意,水的体积增加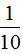 是冰的体积。即水的体积的
是冰的体积。即水的体积的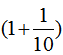 是冰的体积143dm³,已知一个数的几分之几是多少,求这个数,用除法计算,即143÷
是冰的体积143dm³,已知一个数的几分之几是多少,求这个数,用除法计算,即143÷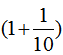 =130(dm³)。
=130(dm³)。
解答:
分步列式:
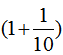 =
=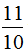 ……(5分)
……(5分)
143÷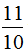 =130(dm³) ……(9分)
=130(dm³) ……(9分)
答:体积是130dm³ ……(10分)
综合列式:
143÷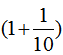 =130(dm³) ……(9分)
=130(dm³) ……(9分)
答:体积是130dm³ ……(10分)
第10题
分析:根据题意,第一双鞋赚了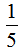 。所以第一双鞋进价的
。所以第一双鞋进价的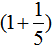 是300元,已知一个数的几分之几是多少,求这个数,用除法计算,即300÷
是300元,已知一个数的几分之几是多少,求这个数,用除法计算,即300÷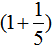 =250(元);第二双鞋亏了
=250(元);第二双鞋亏了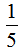 。所以第二双鞋进价的
。所以第二双鞋进价的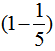 是300元,用除法计算,即300÷
是300元,用除法计算,即300÷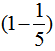 =375(元)。所以两双鞋的总进价为250+375=625(元),实际卖出价为300×2=600(元),625-600=25(元),所以亏了25元。
=375(元)。所以两双鞋的总进价为250+375=625(元),实际卖出价为300×2=600(元),625-600=25(元),所以亏了25元。
解答:
300÷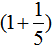 =250(元) ……(3分)
=250(元) ……(3分)
300÷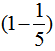 =375(元) ……(6分)
=375(元) ……(6分)
250+375-300×2=25(元) ……(9分)
答:商场亏了,亏了25元。 ……(10分)
第11题
分析:丟番图的一生可以画一个这样的时间轴,如下图所示:

丟番图的时间轴下面5+4=9(年)与上面的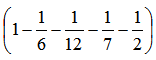 是对应关系,所以丟番图的年龄为
是对应关系,所以丟番图的年龄为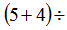
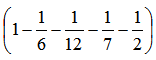 =84(岁)。
=84(岁)。
解答:
分步列式:
5+4=9(年) ……(3分)
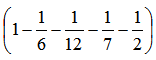 =
=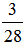 ……(6分)
……(6分)
9÷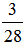 =84(岁) ……(9分)
=84(岁) ……(9分)
答:丟番图的年龄是84岁。 ……(10分)
综合列式:
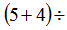
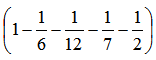 =84(岁) ……(9分)
=84(岁) ……(9分)
答:丟番图的年龄是84岁。 ……(10分)
(5)解决问题(3)
第1题
(1)x+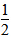 x=180 x=120
x=180 x=120
(2)x-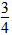 x=120 x=480
x=120 x=480
第2题
解:设这一天北京的黑夜是x小时。
x+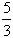 x=24 x=9
x=24 x=9
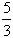 ×9=15(小时)
×9=15(小时)
第3题
解:设上衣花了x元。
x+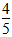 x=180 x=100
x=180 x=100
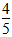 ×100=80(元)
×100=80(元)
第4题
分析:本题可设甲车每小时行驶x千米,乙车的速度是甲车速度的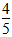 ,则乙车每小时行驶
,则乙车每小时行驶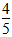 x千米,根据题意:两车6小时共行驶了702千米,根据路程=速度×时间,可列方程为(
x千米,根据题意:两车6小时共行驶了702千米,根据路程=速度×时间,可列方程为(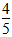 x+x)×6=702,解得x=65,所以
x+x)×6=702,解得x=65,所以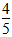 x=52。
x=52。
解答:解:设甲车每小时行驶x千米,则乙车每小时行驶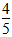 x千米。…………(1分)
x千米。…………(1分)
(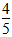 x+x)×6=702…………………(3分)
x+x)×6=702…………………(3分)
x=65…………………(5分)
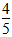 x=52…………………(7分)
x=52…………………(7分)
答:甲车每小时行65千米,乙车每小时行52千米。……………(8分)
第5题
分析:田径队和体操队一共有60人,田径队的人数是体操队人数的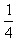 ,也就是田径队的人数=体操队的人数×
,也就是田径队的人数=体操队的人数×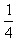 ,或体操队的人数是田径队人数的4倍,所以我们可以设体操队有x人,就可列方程
,或体操队的人数是田径队人数的4倍,所以我们可以设体操队有x人,就可列方程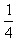 x+x=60,解得x=48,
x+x=60,解得x=48,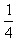 x=12;也可以设田径队有x人,则体操队有4x人,就可列方程x+4x=60,解得x=12,4x=48。根据以上解题思路就可算出王奶奶家养的鹅和鸭的只数,其中鹅和鸭共700只,鹅的只数是鸭的
x=12;也可以设田径队有x人,则体操队有4x人,就可列方程x+4x=60,解得x=12,4x=48。根据以上解题思路就可算出王奶奶家养的鹅和鸭的只数,其中鹅和鸭共700只,鹅的只数是鸭的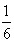 ,所以可以设鸭有x只,则列方程为
,所以可以设鸭有x只,则列方程为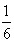 x+x=700,解得x=600,
x+x=700,解得x=600,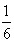 x=100;也可以设鹅有x只,则列方程为x+6x=700,解得x=100,6x=600。
x=100;也可以设鹅有x只,则列方程为x+6x=700,解得x=100,6x=600。
解答:(1)体操队的人数…………………(2分)
(2)体操队的人数 田径队的人数…………………(6分)
(3)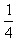 x+x=60 48 12…………………(12分)
x+x=60 48 12…………………(12分)
(4)4x …………………(13分)
解:设田径队有x人,则体操队有4x人。
x+4x=60
x=12…………………(14分)
4x=48…………………(15分)
答:田径队有12人,体操队有48人。…………………(16分)
(5)方法一:解:设鸭有x只,则鹅有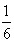 x只。…………………(17分)
x只。…………………(17分)
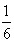 x+x=700
x+x=700
x=600……………(18分)
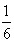 x=100…………………(19分)
x=100…………………(19分)
答:王奶奶家有鹅100只,有鸭600只。……………(20分)
方法二:解:设鹅有x只,则鸭有6x只。…………………(17分)
x+6x=700
x=100…………………(18分)
6x=600…………………(19分)
答:王奶奶家有鹅100只,有鸭600只。……………(20分)
(6)解决问题(4)
第1题
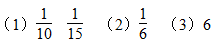
第2题
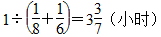
第3题
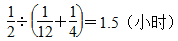
第4题
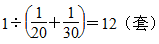
第5题
分析:生产一批玩具,甲厂要12天完成,所以甲厂每天生产玩具总数的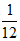 ,乙厂要18天完成,所以乙厂每天生产玩具总数的
,乙厂要18天完成,所以乙厂每天生产玩具总数的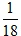 ,甲乙合作3天,一共生产玩具总数的
,甲乙合作3天,一共生产玩具总数的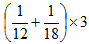 ,还剩玩具总数的
,还剩玩具总数的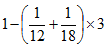 ,剩下的要甲厂单独完成,还需
,剩下的要甲厂单独完成,还需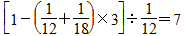 (天)。
(天)。
解答:分步列式:
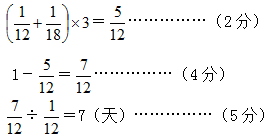
答:还需要7天。……………(6分)
综合列式:
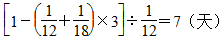
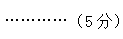
答:还需要7天。……………(6分)
第6题
分析:一项工程,甲队单独做要15天完成,所以甲队每天做这项工程的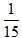 ,乙队单独做要20天完成,所以乙队每天做这项工程的
,乙队单独做要20天完成,所以乙队每天做这项工程的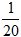 ,丙队单独做要12天完成,所以丙队每天做这项工程的
,丙队单独做要12天完成,所以丙队每天做这项工程的 ,三队合作1天可完成这项工程的
,三队合作1天可完成这项工程的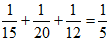 ,2天可完成这项工程的
,2天可完成这项工程的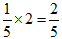 ,还剩下这项工程的
,还剩下这项工程的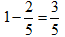 ,若剩下的由甲队单独做还要
,若剩下的由甲队单独做还要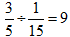 (天);同理若由甲、乙两队合作2天,余下的由乙、丙两队合作,则还需要
(天);同理若由甲、乙两队合作2天,余下的由乙、丙两队合作,则还需要 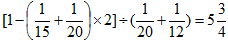 (天);若甲队先做3天,余下的由三队合作,则还需要
(天);若甲队先做3天,余下的由三队合作,则还需要 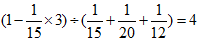 (天);若由甲、丙两队合作2天,余下的由乙队单独做,则还需要
(天);若由甲、丙两队合作2天,余下的由乙队单独做,则还需要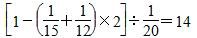 (天)。
(天)。
解答:
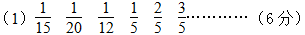
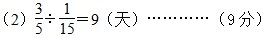
答:还需9天。……………(10分)
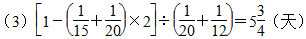

答:还需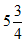 天。……………(15分)
天。……………(15分)
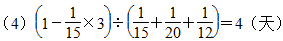
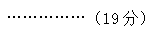
答:还需4天。……………(20分)
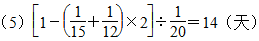

答:还需14天。……………(25分)
