第四章 列举法 - 本章内容
方法概述
1.解决问题时，根据解题的需要，把问题分为不重复、不遗漏的有限情况，一一列举出来并加以分析、解决，最终达到解决整个问题的目的。这种分析、解决问题的方法叫做列举法。列举法也叫枚举法。
2.用列举法解决问题时，常用的方法有表格列举，画图列举和分类列举。
（1）表格列举法。如本书第68页例2的题意分析表格。
（2）画图列举法。如本书第71页例7的题意分析图。
（3）分类列举法。如本书第72页例11的题意分析图。
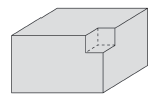
①在一个顶点处挖去一个小正方体。
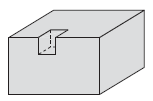
②沿一条棱挖去一个小正方体。
③在某个面挖去一个小正方体。
典例精讲
方法点 一表格列举法
例1 用一根80厘米长的铁丝围成一个长方形，长和宽都是5的倍数。哪一种方法围成的长方形面积最大？
方法指导
要想知道哪种方法围成的长方形面积最大，应将符合条件的围法一一列举出来，然后加以比较。因为长方形的周长是80厘米，所以长与宽的和是40厘米。列表如下：
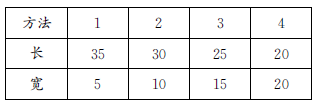
分别求出这四种方法围成的长方形面积，再比较这四个长方形的面积。
正确解答 80÷2=40（厘米）
40=5+35=10+30=15+25=20+20
35×5=175（平方厘米）30×10=300（平方厘米）
25×15=375（平方厘米）20×20=400（平方厘米）
175＜300＜375＜400,所以当长方形的长是20厘米，宽是20厘米时，围成的长方形的面积最大。
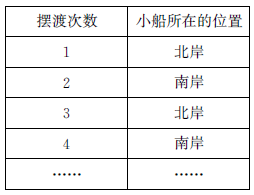
例2 一只小船每天从河的南岸摆渡到北岸，再从北岸摆渡到南岸，不断往返。已知小船最初在南岸。
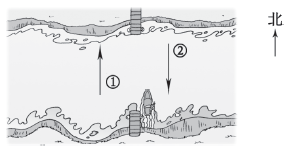
（1）摆渡11次后，小船是在南岸还是在北岸，为什么？
（2）有人说摆渡100次后，小船在北岸。他的说法对吗？为什么？
方法指导
用表格列举出摆渡的次数和小船所在的位置关系，然后观察表格找出摆渡次数与小船所在的位置关系的规律。
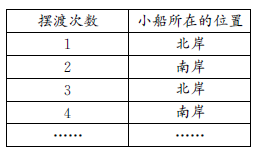
从表中发现：摆渡奇数次后，小船在北岸，摆渡偶数次后，小船在南岸。
正确解答
（1）摆渡11次后，小船在北岸。因为11是奇数，而摆渡奇数次后，小船应在北岸。
（2）他的说法不对。因为100是偶数，而摆渡偶数次后，小船应在南岸。
例3 在我国民间常用十二生肖进行纪年，十二生肖的排列顺序是：鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。2013年是蛇年，2052年是12生肖中的什么年？
方法指导
用表格列举出部分生肖年份。
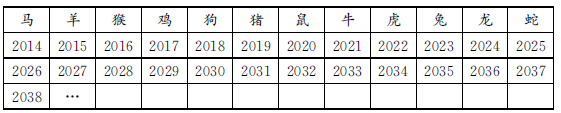
观察上表可以发现，生肖年份每12年是一个周期，用实际年份与2013的差除以周期12，整除时是蛇年，余数是1时是马年，余数是2时是羊年，余数是3时是猴年……
2013年至2052年之间有39年，用39除以12，再根据余数与生肖年份的关系，判定2052年是哪个生肖年。
正确解答 2052-2013=39（年）
39÷12=3（组）……3（年） 2052年是猴年。
答：2052年是12生肖中的猴年。
例4 一个圆柱形盛水容器，从里面量底面积是15平方分米，高是4分米。做一个与这个圆柱形容器容积相同的圆锥形容器，且圆锥的高和底面积都是整数。你知道这个圆锥形容器的底面积和高各是多少吗？
方法指导
圆锥形容器与圆柱形容器的容积相等，先把圆锥的底面积（或者高）看成一个整数，然后用圆柱的容积乘3再除以这个底面积（或者高），即可得出圆锥的高（或底面积）。用表格列举如下：
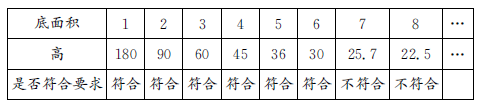
正确解答
15×4×3÷1=180（分米）
15×4×3÷2=90（分米）
15×4×3÷3=60（分米）
15×4×3÷4=45（分米）
15×4×3÷5=36（分米）
15×4×3÷6=30（分米）
15×4×3÷9=20（分米）
……
答：这个圆锥形容器的底面积和高分别是：1平方分米和180分米，2平方分米和90分米，3平方分米和60分米，4平方分米和45分米，5平方分米和36分米，6平方分米和30分米，9平方分米和20分米……
例5 在甲、乙两个仓库存放大米，甲仓库存90袋，乙仓库存50袋，甲仓库每次运出12袋，乙仓库每次运出4袋。运出几次后，两仓库剩下的大米袋数相等？
方法指导
根据题意列表：
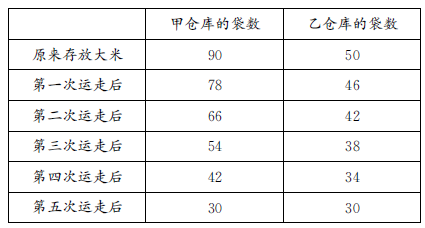
从表中可以看出，每运走一次，两个仓库剩下大米的袋数差就减少8。用两仓库原来存大米袋数差（90-50）除以每次运出后的袋数差，就得出运几次后两个仓库剩下大米的袋数相等。
正确解答 （90-50）÷（12-4）=5（次）
答：运出5次后，两个仓库剩下的大米袋数相等。
方法点二 画图列举法
例6 从A市到B市有3条路，从B市到C市有两条路。从A市经过B市到C市有几种走法？
方法指导
结合示意图把每一种走法一一列举出来。
正确解答
例7 同时掷三枚硬币,求下列事件发生的可能性各是多少。
（1）三枚硬币全部正面朝上。
（2）两枚硬币正面朝上而一枚硬币反面朝上。
（3）至少有两枚硬币正面朝上。
方法指导
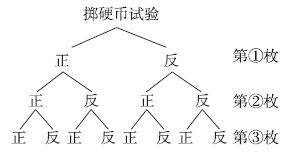
借助树状图进行列举：
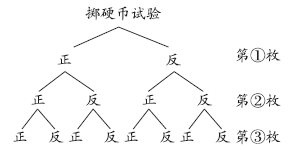
由树状图可以看出,掷3枚硬币的结果共有8种,它们出现的可能性相等。满足三枚硬币全部正面朝上的结果只有1种，满足两枚硬币正面朝上而一枚硬币反面朝上的结果有3种，满足至少有两枚硬币正面朝上的结果有4种。
正确解答
（1）满足三枚硬币全部正面朝上的可能性为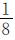
。
（2）满足两枚硬币正面朝上而一枚硬币反面朝上的可能性为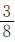
。
（3）满足至少有两枚硬币正面朝上的可能性为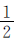
。
方法点三 分类列举法
例8 一根铁丝，第一次剪去它的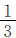
，第二次剪去
米，（）次剪去的长度长一些。
A．第一次B第二次C一样长D无法确定
方法指导
这个题目并没有明确给出铁丝的具体长度，所以要分类进行分析。
（1）如果铁丝的长度是60厘米，那么第一次剪去它的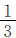就是20厘米，而米就是20厘米，那么两次剪下去的一样长。
（2）如果铁丝的长度小于60厘米大于40厘米，那么第一次剪去全长的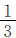就小于20厘米，那么第二次剪去的长。
（3）如果铁丝的长度大于60厘米，那么第一次剪去全长的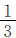就大于20厘米，那么第一次剪去的长。可见选项中的三种答案均有存在的可能。
正确解答 D
例9 四位数7A3B能同时被2、3、5整除，这个四位数可能是多少？
方法指导
先确定B的取值。7A3B能同时被2、5整除，则7A3B是2和5的公倍数，则B为0；因为这个四位数是3的倍数，所以各位数字的和7+3+0+A一定是3的倍数。
（1）当A=2时，10+2=12，四位数为7230;
（2）当A=5时，10+5=15，四位数为7530;
（3）当A=8时，10+8=18，四位数为7830。
正确解答 这个四位数可能是7230，7530或7830。
例10 一个直角三角形的三条边分别长10厘米，8厘米，6厘米，以一条直角边为轴，旋转一周后，得到的圆锥的体积是（）立方厘米。（结果中的π保留，不参与计算）
方法指导
直角三角形的直角边有两条，以不同的直角边为轴进行旋转得到的圆锥的体积不同，此题中直角边为8厘米和6厘米。
（1）以8厘米长的直角边为轴进行旋转，得到的圆锥底面半径是6厘米，高是8厘米。体积是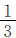×π×6×6×8=96π。
（2）以6厘米长的直角边为轴进行旋转，得到的圆锥底面半径是8厘米，高是6厘米。体积是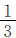×π×8×8×6=128π。
正确解答 96π或128π
例11 从一个长10厘米,宽6厘米,高5厘米的长方体木块上挖去一个棱长为2厘米的小正方体,剩下部分的表面积是多少?
方法指导
在大长方体上挖去一个小正方体，所选位置不同，所剩的表面积也不同。
正确解答
（1）如图所示，在一个顶点处挖去一个小正方体，长方体的表面积不变。
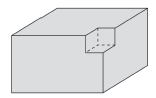
（6×5+6×10+5×10）×2
=140×2
=280（平方厘米）
（2）如图所示，沿一条棱挖去一个小正方体，表面积比原来多了2个正方形的面。
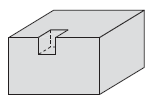
（6×5+6×10+5×10）×2+2×2×2
=140×2+8
=280+8
=288（平方厘米）
（3）如图所示，在某个面挖去一个小正方体，表面积比原来多了4个正方形的面。
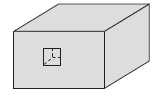
（6×5+6×10+5×10）×2+2×2×4
=280+16
=296（平方厘米）
答：剩下部分的表面积可能是280平方厘米、288平方厘米或296平方厘米。
例12 现在有一张长40厘米、宽20厘米的长方形铁皮，请你用它做一个高5厘米的长方体无盖铁皮盒（焊接处及铁皮厚度忽略不计）你做出的铁皮盒容积是多少立方厘米？
正确解答
（1）在铁皮的四角剪去边长为5厘米的正方形，做成的无盖铁皮盒长是40-5×2=30（厘米），宽是20-5×2=10（厘米），高是5厘米。
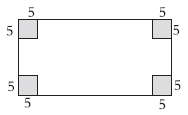
体积：（40-5×2）×（20-5×2）×5
=30×10×5
=1500（立方厘米）
（2）在铁皮的一侧角上剪下两个边长为5厘米的正方形，焊接到铁皮另一侧的中间位置，这样做成的无盖铁皮盒长是40-5=35（厘米），宽是20-5×2=10（厘米），高是5厘米。
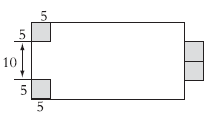
体积：（40-5）×（20-5×2）×5=1750（立方厘米）
（3）在铁皮的两侧各剪下一条宽为5厘米、长为20厘米的长方形铁皮分别焊到上、下边的中间部位，这样做成的无盖铁皮盒长也就是焊到中间部位的铁皮的长，是20厘米，宽是20厘米，高是5厘米。
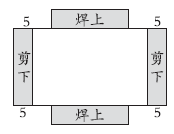
体积：20×20×5=2000（立方厘米）
所以铁皮盒容积可能是1500立方厘米、1750立方厘米和2000立方厘米。
例13 用四个棱长为3厘米的正方体拼成长方体，长方体的表面积是多少平方厘米？
正确解答
（1）拼法一，如下图：
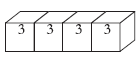
表面积：3×4=12（厘米）
12×3×4+3×3×2
=144+18
=162（平方厘米）
（2）拼法二，如下图：
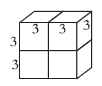
表面积：3×2=6（厘米）
6×6×2+3×6×4
=72+72
=144（平方厘米）
答：长方体的表面积是162平方厘米或144平方厘米。
例14 如下图，平面上有16个点，可任意取其中四个点围成一个正方形，这样的正方形有多少个？
方法指导
（1）如图所示，这种围法围成的正方形共有14个。
（2）如图所示，这种围法围成的正方形有4个。
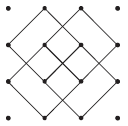
（3）如图所示，这种围法围成的正方形有2个。
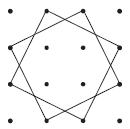
正确解答 14+4+2=20（个）
答：这样的正方形有20个。