2.长方体和正方体的表面积 - (2)长方体的表面积
第1题
(1)30 24 20 148 (2)ab+2ah
(3)12 dm2
第2题
(1)× (2)√ (3)×
第3题
(1)长:1×3=3(cm) 宽:1×2=2(cm)
高:1×2=2(cm)
表面积:(3×2+3×2+2×2)×2=32(cm2)
(2)(1.2×0.8+0.8×0.6+1.2×0.6)×2=4.32(cm2)
第4题
(6×4+6×2+4×2)×2=88(cm2)
第5题
120×40×4=19200(cm2)
19200 cm2=1.92 m2 1.92×10=19.2(m2)
第6题
(5+6+5)×2=32 (cm2)
第7题
分析:本题考查的就是长方体的表面积,即长方体的表面积=(长×宽+宽×高+长×高)×2。首先明确求做一个这样的储水箱至少需要多少平方米铁皮,就是求少一个上底面的长方体的表面积。因为底面是一个边长为3 dm的正方形,所以只需要求出4个相等侧面的面积与一个底面的面积,即长方体储水箱的表面积。
解答:分步列式:
3 dm=0.3 m……………(1分)
0.3×0.3=0.09(m2) ……………(2分)
0.3×1.8×4=2.16(m2) ……………(3分)
0.09+2.16=2.25(m2) ……………(2分)
答:做一个这样的储水箱至少需要2.25 m2铁皮。……………(1分)
或列综合算式:
3 dm=0.3 m……………(1分)
0.3×0.3+0.3×1.8×4=2.25(m2) ……………(7分)
答:做一个这样的储水箱至少需要2.25 m2铁皮。……………(1分)
第8题
(18×20+20×12)×2+3×20=1260(cm2)
第9题
分析:如果要使这两个小长方体的表面积的和最大,那么就得使增加的两个小长方体的横截面的面积最大,三个不同的面中长是7 cm,宽是6 cm的面积最大。只要把4条高沿同一水平面截断,增加的两个面就最大。如图所示: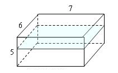 ,截成的两个小长方体的表面积=原来长方体的表面积+增加的两个面的面积。
,截成的两个小长方体的表面积=原来长方体的表面积+增加的两个面的面积。
解答:分步列式:
(7×6+7×5+6×5)×2=214(cm2) ……………(3分)
7×6×2=84(cm2) ……………(3分)
214+84=298(cm2) ……………(3分)
答:这两个小长方体的表面积之和最大是298 cm2。……………(1分)
或列综合算式:
(7×6+7×5+6×5)×2+7×6×2=298(cm2) ……………(9分)
答:这两个小长方体的表面积之和最大是298 cm2。……………(1分)
第10题
(1)拼法一: 5 3 4……………(3分)
拼法二:10 3 2……………(3分)
拼法三:6 5 2……………(3分)
(2)分析:可以直接根据长方体的表面积计算公式计算表面积,也可以先算出原来两个长方体的表面积之和,再减去减少的两个面的面积。重合在一起的两个面的面积越小,拼成的大长方体的表面积越大;重合在一起的两个面的面积越大,拼成的大长方体的表面积越小。
解答:拼法一的表面积:5×3×2+5×(2+2)×2+3×(2+2)×2=94(dm2)
或(5×3+5×2+3×2)×2×2-5×3×2=94(dm2) ……………(2分)
拼法二的表面积:(5+5)×3×2+(5+5)×2×2+3×2×2=112(dm2)
或(5×3+5×2+3×2)×2×2-3×2×2=112(dm2) ……………(2分)
拼法三的表面积:5×(3+3)×2+5×2×2+(3+3)×2×2=104(dm2)
或(5×3+5×2+3×2)×2×2-5×2×2=104(dm2) ……………(2分)
拼法二的大长方体的表面积最大,拼法一的大长方体的表面积最小。……………(2分)
