学霸易错题 - 三 分数除法
易错点1 单位“1”的量混淆
例1 小敏养了一些金鱼,红金鱼的条数是黄金鱼的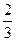 ,黄金鱼的条数是黑金鱼的
,黄金鱼的条数是黑金鱼的 。黄金鱼有12条,红金鱼和黑金鱼各有多少条?
。黄金鱼有12条,红金鱼和黑金鱼各有多少条?
错解 12×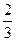 =8(条) 12×
=8(条) 12× =9(条)
=9(条)
答:红金鱼有8条,黑金鱼有9条。
错因剖析 此题错在求黑金鱼的数量时没有正确确定单位“1”的量。在“黄金鱼的条数是黑金鱼的 ”中,黑金鱼的条数是单位“1’,是未知量。已知部分量和部分量所对应的分率,求单位”1”的量,用除法计算。
”中,黑金鱼的条数是单位“1’,是未知量。已知部分量和部分量所对应的分率,求单位”1”的量,用除法计算。
正确解答 12×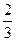 =8(条) 12÷
=8(条) 12÷ =16(条)
=16(条)
答:红金鱼有8条,黑金鱼有16条。
点拨 解题时要认真比较,找准单位“1”及它所对应的分率,正确解答。
跟踪练习
1.赵老师的讲桌上有红粉笔16支,白粉笔的支数是红粉笔的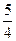 ,又是蓝粉笔的
,又是蓝粉笔的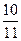 。蓝粉笔有多少支?
。蓝粉笔有多少支?
2.小明写单词36个,是小兰写的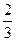 ,是小红写的
,是小红写的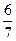 ,小兰比小红多写多少个单词?
,小兰比小红多写多少个单词?
3.丽湖风景区有白天鹅100只,是黑天鹅总数的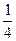 ,黑天鹅的只数又是水鸭只数的
,黑天鹅的只数又是水鸭只数的 。白天鹅、黑天鹅和水鸭一共有多少只?
。白天鹅、黑天鹅和水鸭一共有多少只?
答案 1.16×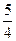 ÷
÷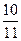 =22(支)
=22(支)
2.36÷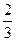 -36÷
-36÷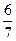 =12(个)
=12(个)
3.100+100÷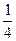 +100÷
+100÷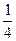 ÷
÷ =1400(只)
=1400(只)
易错点2 “已知一个数的几分之几是多少,求这个数”与“求一个数的几分之几是多少”存在误区
例2 冰化成水后,水的体积是冰的体积的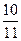 。现有一块冰,化成水的体积是33立方分米,这块冰的体积是多少立方分米?
。现有一块冰,化成水的体积是33立方分米,这块冰的体积是多少立方分米?
错解 33×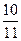 =30(立方分米)
=30(立方分米)
错因剖析 此题错在没能正确找出单位“1”。冰化成水和水结成冰单位“1”是不同的。冰化成水是以“冰的体积”为单位“1”,而水结成冰是以“水的体积”为单位“1”。已知水的体积是冰的体积的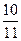 ,求冰体积,是求单位“1”的量,应该用除法计算。
,求冰体积,是求单位“1”的量,应该用除法计算。
正确解答 33÷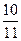 =
=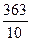 (立方分米)
(立方分米)
答:这块冰的体积是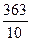 立方分米。
立方分米。
点拨 已知一个数的几分之几是多少,求这个数,用除法计算。
跟踪练习
1.冰化成水后,水的体积是冰的体积的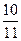 。现有一块冰,体积是33立方分米,这块冰化成水的体积是多少立方分米?
。现有一块冰,体积是33立方分米,这块冰化成水的体积是多少立方分米?
2.在通常情况下,体积相等的冰的质量比水的质量少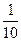 。现有一块重9kg的冰,如果有一桶水的体积和这块冰的体积相等,这桶水有多重?
。现有一块重9kg的冰,如果有一桶水的体积和这块冰的体积相等,这桶水有多重?
3.冰化成水后,水的体积是冰的体积的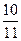 。现有一块冰,化成水以后的体积是30立方分米,这块冰的体积是多少立方分米?
。现有一块冰,化成水以后的体积是30立方分米,这块冰的体积是多少立方分米?
答案 1.33×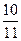 =30(立方分米)
=30(立方分米)
2.9÷(1-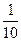 )=10(kg)
)=10(kg)
3.30÷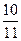 =33(立方分米)
=33(立方分米)
易错点3 对分数除法的意义理解不透彻
例3 一辆汽车行8 km耗油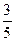 L,平均每行1千米要耗油( )L,平均每升汽油可以行驶( )千米。
L,平均每行1千米要耗油( )L,平均每升汽油可以行驶( )千米。
错解 平均每行1千米要耗油(8÷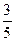 =
=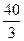 )L。
)L。
平均每升汽油可以行驶(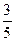 ÷8=
÷8=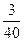 )km。
)km。
错因剖析 此题错在没有正确理解题意,只是知道用除法,但却不知道谁除以谁。求平均每行1千米要耗油多少升,是用“千米数”作除数;求平均每升汽油可以行驶多少千米,是用“耗油数”作除数。
正确解答 平均每行1千米要耗油(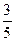 ÷8=
÷8=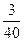 )L。
)L。
平均每升汽油可以行驶(8÷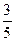 =
=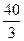 )km。
)km。
点拨 遇到这类问题时,要先分清哪是总量,哪是份数,再解答。
跟踪练习
1.一根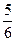 m长的钢管重5kg,这种钢管平均每米重多少千克?平均每千克钢管有多少米?
m长的钢管重5kg,这种钢管平均每米重多少千克?平均每千克钢管有多少米?
2.小强走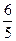 km要用
km要用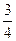 小时,他平均每小时走( )km;他平均每走1km要用( )小时。
小时,他平均每小时走( )km;他平均每走1km要用( )小时。
3.刘伟平均步行1km要用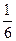 小时,1小时能走( )km;小刚骑自行车每小时行15 km,平均行1 km要用( )小时。
小时,1小时能走( )km;小刚骑自行车每小时行15 km,平均行1 km要用( )小时。
答案 1.5÷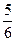 =6(kg)
=6(kg) 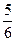 ÷5=
÷5=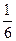 (m)
(m)
2.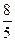
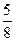
3.6 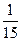
易错点4 审题不认真,单位“1”的量确定不正确
例4 一个机械加工厂,九月份生产一种零件1000个,比原计划多生产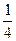 。多生产多少个零件?
。多生产多少个零件?
错解 1000×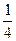 =250(个)
=250(个)
答:多生产250个零件。
错因剖析 此题错在单位“1”的量确定错误。“比原计划多生产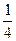 ”应把原计划要生产的数量看作单位“1”。“1000个零件”是实际生产的数量。所以要先求出单位“1”的量,即原计划生产零件的数量,再求出多生产多少个零件。
”应把原计划要生产的数量看作单位“1”。“1000个零件”是实际生产的数量。所以要先求出单位“1”的量,即原计划生产零件的数量,再求出多生产多少个零件。
正确解答 1000÷(1+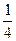 )=1000÷
)=1000÷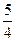 =800(个)
=800(个)
1000-800=200(个)或800×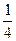 =200(个)
=200(个)
答:多生产200个零件。
点拨 解答此类问题,在找准单位“1”的同时,还要明确所求问题与单位“1”的关系。
跟踪练习
1.今年生产电冰箱24000台,比去年多生产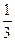 ,多生产电冰箱多少台?
,多生产电冰箱多少台?
2.白兔有420只,黑兔比白兔少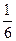 ,黑兔比白兔少多少只?
,黑兔比白兔少多少只?
3.海华电器集团今年生产电视机36000台,比去年少生产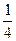 ,今年比去年少生产多少台?
,今年比去年少生产多少台?
答案 1.24000÷(1+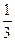 )×
)×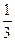 =6000(台)
=6000(台)
2.420×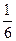 =70(只)
=70(只)
3.36000÷(1-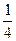 )×
)×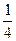 =12000(台)
=12000(台)
易错点5 工作效率概念模糊
例5 一项工作,小华单独做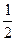 小时完成,小明单独做
小时完成,小明单独做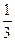 小时完成,如果两人合做,( )小时完成。
小时完成,如果两人合做,( )小时完成。
错解 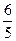
错因剖析 此题错在把题中的“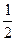 小时”和“
小时”和“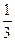 小时”看成工作效率,这是小华和小明单独完成这项工作所用的时间,这里把工作总量看作单位“1”,则小华的工作效率是1÷
小时”看成工作效率,这是小华和小明单独完成这项工作所用的时间,这里把工作总量看作单位“1”,则小华的工作效率是1÷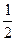 =2,小明的工作效率是1÷
=2,小明的工作效率是1÷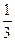 =3,工作总量÷工作效率和=合做时间。
=3,工作总量÷工作效率和=合做时间。
正确解答 1÷(1÷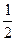 +1÷
+1÷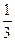 )=
)=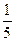
点拨 在解决工程问题时,要弄清楚工作效率是工作总量除以工作时间得到的。
跟踪练习
1.一条水渠长3.3米,甲单独修完要5小时,乙单独修完要6小时。两人合做,几小时修完?
2.一项工程,甲队单独做要15天完成,乙队单独做要10天完成。两队合做3天后,剩下的由甲队完成,甲队还要多少天才能完成这项工程?
3.一项工程,如果甲、乙合做,那么两天能完成这项工程的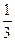 。如果甲单独做,那么10天能完成这项工程。现在由乙单独做,几天能完成这项工程?
。如果甲单独做,那么10天能完成这项工程。现在由乙单独做,几天能完成这项工程?
答案 1.1÷(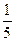 +
+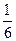 )=
)=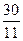 (时)
(时)
2.[1-(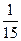 +
+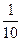 )×3]÷
)×3]÷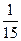 =7.5(天)
=7.5(天)
3. 1÷(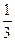 ÷2-
÷2-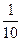 )=15(天)
)=15(天)
