四年级数学（上册） - 三 角的度量
1.线段 直线 射线
第1题
①⑦ ④⑥ ②⑧
第2题
（1）①C ②A B ③B
（2）①C ②A
第3题
（1）× （2）× （3）× （4）√
第4题
（1）A B C （2）A
第5题
（1）
（2）6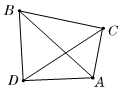 
第6题
分析：（1）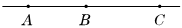
图中共有三个端点。任选两个端点便可组成一条线段，即AB、AC、BC，共3条线段；任选一个端点向左、向右可分别引出一条射线，即射线AB、射线BA、射线AC、射线CA、射线BC、射线CB，共6条射线；而直线是没有端点的，所以只有1条。
（2）
图中共有5个端点，任选两个端点便可组成一条线段，即AB、AC、AD、AE、BC、BD、BE、CD、CE、DE,共10条线段。
解答：（1）1 6 3……（6分）
（2）10……（6分）
2．角
第1题
（1）射线 角 （2）∠ （3）射
第2题
（1）
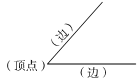
（2）∠1 角1
第3题
①③⑤⑥
第4题
分析：一个正方形有4个直角，如果去掉一个角，有三种情况，如图：
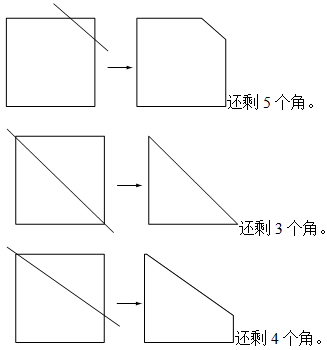
解答：一个正方形有4个角，如果去掉一个角，还剩3个、4个或5个角。……（8分）
第5题
分析：（1）如图，图中角分别是: ∠AOB，∠AOC，∠AOD，∠AOE，∠BOC，∠BOD，∠BOE，∠COD，∠COE，∠DOE，共10个。
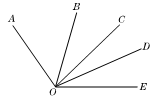
数角的个数时，要按着方向有规律的数，也可以记住一个公式：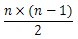
（n代表线段的条数）。本题中有5条线段，n代表5，角的个数为
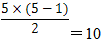（个）。此公式只适合有一个公共端点的线段组成的角。
（2）如图，图中的角分别是：∠BAD，∠ABD，∠ABC，∠DBC，∠BCD，∠ADB，∠ADC，∠BDC，共8个。
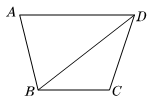
解答：（1）10……（5分）
（2）8……（5分）
3.角的度量
第1题
（1）1度 1° 量角器 （2）度 °
第2题
小明（√）
第3题
（1）B…………（3分）
（2）分析：角的大小与角的两边的长短无关，只与角的两边张开的大小有关。所以此题中角的度数不变。
解答：A…………（3分）
（3）C…………（3分）
（4）分析：钟表上的时针、分针转动一周为360°，而钟面上的12个点将这360°平均分成了12份，即12个大格，每个大格就是30°，根据题中妈妈的话“分针走了60°，水就开了。”说明分针要转动2个大格，也就是转到2时水就开了，共用了10分钟，所以妞妞应该在9时10分提醒妈妈。
解答：B…………（3分）
第4题
180°
第5题
分析：通过测量得出各角的度数，如图：
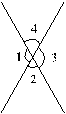
∠1＝120°，∠2＝60°，∠3＝120°，∠4＝60°。
如图：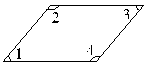
∠1＝50°,∠2＝130°,∠3＝50°,∠4＝130°。
解答：∠1＝120° ∠2＝60° ∠3＝120° ∠4＝60°
∠1＝50° ∠2＝130° ∠3＝50° ∠4＝130°……（16分）
我发现：（1）第一幅图中，相对的角度数相等，相邻的角度数相加的和是180°……（16分）。
（2）第二幅图中，相邻的角度数相加的和是180°，相对的角度数相等。……（4分）
4．角的分类
第1题
（1）× （2）× （3）×
（4）√ （5）×
第2题
④⑦ ① ⑥ ③⑧ ②⑤
第3题
锐角：75° 88° 89° 59° 60°
直角：90°
钝角：135° 91° 179° 100°
平角：180°
周角：360°
第4题
（1）4 （2）2 4
（3）45 锐 （4）156
（5）钝
（6）锐角 直角 钝角 平角 周角
（7）60° （8）钝
第5题
45° 锐角
第6题
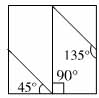
分析：（1）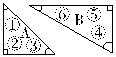
图中画的是两副直角三角板。
图A的三角板是等腰直角三角板，可知∠2＝90°，∠1＝∠3＝45°。
图B的三角板是直角三角板，可知∠5＝90°，∠6＝30°，∠4＝60°。
根据：①小于90°的角是锐角，②大于90°而小于180°的角是钝角，③等于90°的角是直角，④等于180°的角是平角，
可以推出：
①+⑤＝45°+90°＝135°，是钝角。
④－③＝60°－45°＝15，是锐角。
⑥+①+④＝30°+45°+60°＝135°，是钝角。
②+⑤＝90°+90°＝180°，是平角。
①+③＝45°+45°＝90°，是直角。
（2）⑤+③＝90°+45°＝135°，
180°－④＝180°－60°＝120°。
解答：（1）
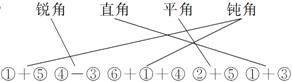……（5分）
（2） 135 120……（6分）
第7题
分析：
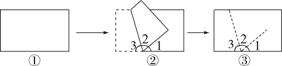
长方形的四个角都是直角。
长方形的四个角的度数和是360°。
将长方形的一边向上折以后，如图②，实际上是∠2和∠3是相等的，展开之后如图③，由此推出：∠3+∠2+∠1＝180°，因为∠1＝40°，
所以2∠2＝180°－40°
∠2＝140°÷2
∠2＝70°。
解答：四个角都是直角……（1分）
四个角度数的和是360°………（1分）
因为∠1+2∠2＝180……（3分）
所以∠2＝（180－∠1）÷2
＝（180°－40°）÷2
＝70°……（3分）
第8题
分析：要想解决这样的问题，必须理解、知道钟面上的时针、分针转动一周是360°，分针、时针每走一个大格，就是转动了30°。左侧钟表显示的是5时整，分针和时针所形成的角中有5个大格，即有5个30°，就是150°，所以左侧钟表时针和分针所形成的角是150°，它是大于90°而小于180°的角，所以是钝角。右侧钟表当时针和分针重合时，就成了周角，也就是12时整，分针和时针成周角。
解答：150° 钝 12：00 360
第9题
分析：这道题要求我们看图判断锐角、直角、钝角的个数。要想准确判断就要熟练掌握什么是锐角、直角、钝角。小于90°的角是锐角；等于90°的角是直角；大于90°而小于180°的角是钝角。
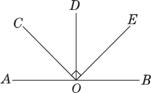通过观察，我们可以判断出：
∠AOD、∠COE、∠DOB是直角，共3个。
∠AOE、∠COB是钝角，共2个。
∠AOC、∠COD、∠DOE、∠EOB是锐角，共4个。
解答：4 3 2
第10题
分析：（1）根据题意可知∠1＝∠2＝∠3，图中所有角的度数和是150°，图中所有的角分别是：∠1，∠BOD，∠BOA,∠2，∠COA，∠3共6个角。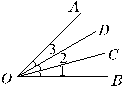
（2）通过观察图形可知，∠BOD＝2∠1，∠BOA＝3∠1，∠COA＝2∠2，由此可以推出
∠BOC+∠BOD+∠BOA+∠COD+∠COA+∠AOD
＝∠1+2∠1+3∠1+∠2+2∠2+∠3
＝10∠1（相当于10个∠1）。
又因为10∠1＝150°，
所以∠1＝15°，
即∠1＝∠2＝∠3＝15°。
（3）所以∠AOB＝3∠1＝15×3＝45°。
（4）根据题意已知∠1＝∠2＝∠3＝∠4，图中所有的角的和是300°，图中所有的角分别是：
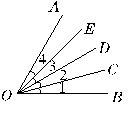∠1、∠BOD、∠BOE、∠BOA；
∠2、∠COE、∠COA；
∠3、∠DOA；
∠4，共有10个角。
通过已知条件可知∠BOD＝2∠1，∠BOE＝3∠1，∠BOA＝4∠1，∠COE＝2∠2，∠COA＝3∠2，∠DOA＝2∠3,
∠BOC+∠BOD+∠BOE+∠BOA+∠COD+∠COE+∠COA+∠DOE+∠DOA+∠AOE
＝∠1+2∠1+3∠1+4∠1+∠2+2∠2+3∠2+∠3+2∠3+∠4
＝20∠1（相当于20个∠1）。
又因为20∠1＝300°，
即∠1＝300°÷20，
所以∠1＝15°。
所以∠AOB＝4∠1＝4×15°＝60°。
解答：（1）6 （2）10 15
（3）45
（4）因为∠1＝∠2＝∠3＝∠4，且图中所有角的度数和为300°……（1分）
所以20∠1＝300，即∠1＝15°……（5分）
所以∠AOB＝4∠1＝4×15°＝60°……（2分）
5．画 角
第1题
（1）射线 中心 射线 0°
（3）端点 射线
第3题
（画法不唯一）
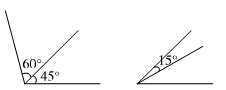
第5题
分析：此题可动手操作，折一折，画一画。
……（6分）
第6题
分析：（1）如图，因为50°+∠4＝180°，
所以∠4＝180°－50°，
即∠4＝130°。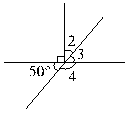
又因为∠4+∠3＝180°，
即130°+∠3＝180°，
所以∠3＝180°－130°，
即∠3＝50°。
因为∠2+∠3＝90°，
即∠2+50°＝90°
所以∠2＝90°－50°，
即∠2＝40°。
或因为∠2+∠3+90°＝180°，
所以∠2＝180°－（50°+90°）
＝180°－140°
＝40°。
（2）如图：因为∠2＝40°，∠3＝90°，所以∠2+∠3＝40°+90°＝130°。
因为∠2+∠3+∠4＝180°，
所以∠4＝180°－∠2－∠3
＝180°－90°－40°
＝50°。
所以∠3+∠4＝90°+50°＝140°。
因为∠1＝180°，
所以∠1+∠2+∠4＝180°+40°+50°＝270°，
∠1+∠3+∠4＝180°+90°+50°＝320°。
解答：（1） ∠2＝40°，∠3＝50°，
∠4＝130°，∠2+∠4＝170°。
（2）∠2+∠3＝130°，∠3+∠4＝140°，
∠1+∠2+∠4＝270°，
∠1+∠3+∠4＝320°。